如图所示，在同一竖直平面内，一轻质弹簧一端固定，另一自由端恰好与水平线AB齐平，静止放于光滑斜面上，一长为L的轻质细线一端固定在O点，另一端系一质量为m的小球，将细线拉至水平，此时小球在位置C，由静止释放小球，小球到达最低点D时，细绳刚好被拉断，D点到AB的距离为h，之后小球在运动过程中恰好沿斜面方向将弹簧压缩，弹簧的最大压缩量为x，重力加速度为g.求：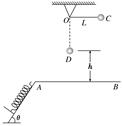

(1)细绳所能承受的最大拉力；
(2)斜面的倾角θ的正切值；
(3)弹簧所获得的最大弹性势能．

(1)3mg　(2)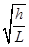　(3)mg(x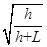＋h＋L)

解析试题分析：(1)小球由C到D，机械能守恒mgL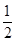＝mv12，
v1＝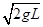
在D点，F－mg＝m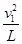，F＝3mg
由牛顿第三定律知，细绳所能承受的最大拉力为3mg.
(2)小球由D到A做平抛运动
vy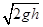＝，tanθ＝＝.
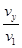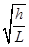(3)小球到达A点时
vA2＝vy2＋v12＝2g(h＋L)
在压缩弹簧的过程中小球与弹簧组成的系统机械能守恒Ep＝mgxsinθ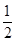＋mvA2
所以Ep＝mg(x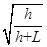＋h＋L)．
考点：功能关系；牛顿第二定律；机械能守恒定律．
点评：本题是圆周运动、平抛运动、机械能守恒的综合，情景简单，应按程序进行分析和求解．

关闭