如图所示，斜面倾角为37°，质量为1kg的物体静止在斜面底端，物体与斜面的滑动摩擦系数μ=0.5，某时刻有一平行于斜面向上的20N的外力作用在物体上，2秒后外力撤去．求：（1）撤去外力的瞬间物体的速度大小；（2）物体能继续向上滑行的距离（假设斜面足够长）；（3）物体最后能否静止在斜面上？如果不能，请求出物体从撤去外力开始到滑回斜面底端所用的时间．
分析：（1）由物体的受力可以求得其撤去外力前的加速度，由运动学可以求得撤去时的速度．
（2）撤去后其余受力不变，由此可以求得加速度，进而求得上滑距离
（3）比较重力沿斜面的分力与摩擦力的大小可以知道，物体不能静止．由（2）的已知量可以求得撤去后上滑的时间，然后再求下滑时间：先求出撤去前的位移和撤去后的上滑位移，两者之和为总位移．物体向下做匀加速直线运动，故而可以求得下滑时间，两者相加即为总时间．
解答：解：

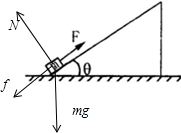
（1）对物体受力分析如图，由牛顿第二定律：
F-mgsin37°-μmgcos37°=ma1
解得：
a1=10m/s2
又：
v1=a1t=20m/s
（2）撤去F之后，其余受力不变，故而由牛顿第二定律：
mgsin37°+μmgcos37°=ma2
解得：
a2=10m/s2
又滑行到最高点速度为零：
x2=
v12
2a2
=20m
（3）由于 mgsin37°=6N，μmgcos37°=4N，故：mgsin37°＞μmgcos37°所以物体不能静止
撤去外力后上升时间：t2=
v1
a2
=2s
撤去之前的位移为：
x1=
v1
2
t=20m
上升的总位移：
x=x1+x2=40m
在下降阶段由牛顿第二定律：
mgsin37°-μmgcos37°=ma3
解得：
a3=2m/s2
由：
x=
1
2
a3t32
解得：
t3=2
10
s
故从撤去外力开始到滑回斜面底端所用的时间为：
t=t2+t3=(2+2
10
)s
答：
（1）撤去外力的瞬间物体的速度20m/s
（2）物体能继续向上滑行的距离20m
（3）不能，从撤去外力开始到滑回斜面底端所用的时间(2+2
10
)s
点评：本题关键是要掌握好受力分析和运动分析，这两个分析能力是牛顿第二定律应用的基础，只有熟练掌握才能应对牛顿第二定律的应用．
关闭