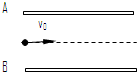
如图所示，质量为m=5×10-8kg的带电粒子以v0=2m/s的速度从水平放置的平行金属板A、B中央飞入电场，已知板长L=10cm，板间距d=2cm，当AB间加电压UAB=103V时，带电粒子恰好沿直线穿过电场（设此时A板电势高），重力加速度取g=10m/s2求：
（1）粒子带什么电？电荷量为多少？
（2）A、B间所加电压为多少时，带电粒子刚好能从上极板右端飞出？
分析：（1）、因带电粒子在电场中直线穿过，所以受到的电场力和重力大小相等、方向相反，所以电场力向上，又因A板电势高，所以带电粒子带负电．由二力平衡列式可求出带电粒子的带电量．
（2）、根据初速度大小和板的长度，可求出带电粒子在板间的运动时间，因要求粒子刚好从上极板右端飞出，此时的位移式
d
2
，结合运动学公式和牛顿第二定律列式可求出此时的电压．
解答：解：
（1）、当AB间加电压UAB=103V时，带电粒子恰好沿直线穿过电场，可知带电粒子受到的重力和电场力是一对平衡力，电场力向上，由题意知电场的方向向下，所以带电粒子带负电．
由平衡条件有：
qU
d
=mg…①
得：q=
mgd
u
=
5×10-8 ×10×0.02
103
=1×10-11C…②
（2）、粒子飞越时间t=
L
v0
=
0.1
2
=0.05s
当带电粒子刚好能从上极板右端飞出时，位移是
d
2
，设加速度为a，则由运动学公式有：
d
2
=
1
2
a t2
得：a=
d
t2
=8m/s2
 对带电粒子进行受力分析，受重力和电场力作用，设此时的电场力为F，由牛顿第二定律有：
F-mg=ma
得：F=ma+mg=9×10-7N，
又有F=qE=q
U
d

以上各式联立的U=1800V．
答：（1）粒子带负电，电荷量为1×10-11C．
（2）A、B间所加电压为1800V时，带电粒子刚好能从上极板右端飞出．
点评：带电粒子在电场中的偏转问题：
（1）由带电粒子在电场中的运动轨迹分析有关的问题：分析这类问题关键是要根据轨迹弯曲的方向，确定粒子所受电场力的方向，进而利用分析力学问题的方法分析其他有关问题．
（2）带电粒子在匀强电场中类平抛的偏转问题：
①运动状态分析：带电粒子以速度v0垂直于电场线方向飞入匀强电场时，受到恒定的与初速度方向成90°角的电场力作用而做匀变速曲线运动（轨迹为抛物线）
②偏转运动的分析处理方法（用类似平抛运动分析方法）．
沿初速度方向为速度为v0的匀速直线运动；
沿电场力方向为初速度为零的匀加速运动．
③基本公式：
加速度：a=
F
m
=
qE
m
=
qU
md
              
飞行时间：t=
l
v0
侧移距离：y=
1
2
(
qU
md
)(
l
v0
)2  =
qUl2
2m
v
2
0
d
偏转角度：tanθ=
vy
vx
=
at
v0
=
qUl
m
v
2
0
d
关闭