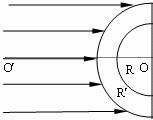
精英家教网如图所示，用折射率n=
2
的玻璃做成内径为R、外径为R′=
2
R的半球形空心球壳，一束平行光射向此半球的外表面，与中心对称轴OO'平行，试求：
（1）球壳内部有光线射出的区域；
（2）要使球壳内部没有光线射出，至少用多大的遮光板，如何放置才行？
分析：（1）光线射到内球面时，若入射角大于或等于临界角时，会发生全反射，光线将不能射入球壳内部．根据折射定律求出临界角．作出光路图，由几何知识求出光线射到内球面刚好发生全反射时，在外球面的折射角，由数学知识求出球壳内部有光线射出的区域．
（2）根据光路图，由几何知识求出遮光板的大小，确定如何放置．
解答：解：（1）设光线a′a射入外球面，沿ab方向射向内球面，精英家教网
刚好发生全反射，则
   sinC=
1
n
=
1
2

∴C=45°
在△Oab中，Oa=
2
R，Ob=R
根据数学知识得
sin(180°-C)
2
R
=
sinr
R
，
得到sinr=
sinC
2
=
1
2

即 r=30°，则∠θ=C-r=45°-30°=15°
又∠O′Oa=i，由
sini
sinr
=n，得sini=nsinr=
2
2

∴i=45°
即∠O′Ob=i+θ=45°+15°=60°
当射向外球面的入射光线的入射角小于i=45°时，这些光线都会射出内球面．因此，以OO'为中心线，上、下（左、右）各60°的圆锥球壳内有光线射出．
（2）由图中可知，h=R′sini=
2
R•
2
2
=R，
所以，至少用一个半径为R的遮光板，圆心过OO′轴并垂直该轴放置，才可以挡住射出球壳的全部光线，这时球壳内部将没有光线射出．
答：
（1）球壳内部有光线射出的区域为以OO′为中心线，上、下（左、右）各60°的圆锥球壳内有光线射出．
（2）要使球壳内部没有光线射出，至少用一个半径为R的遮光板，圆心过OO'轴并垂直该轴放置．
点评：本题是折射定律、临界角和几何知识的综合应用，作出光路图是基础．
关闭