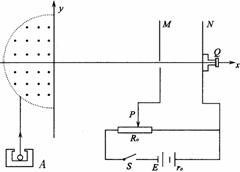
如图所示，某放射源A中均匀地向外辐射出平行于y轴的、速度一定的α粒子(质量为m，电荷量为+q)．为测定其飞出的速度大小，现让其先经过一个磁感应强度为B、区域为半圆形的匀强磁场，经该磁场偏转后，它恰好能够沿x轴进人右侧的平行板电容器，并打到置于N板上的荧光屏上。调节滑动触头，当触头P位于滑动变阻器的中央位置时，通过显微镜头Q看到屏上的亮点恰好能消失．已知电源电动势为E，内阻为r0，滑动变阻器的总阻值R0=2 r0，问：（1）α粒子的速度大小υ0=?

  （2）满足题意的α粒子，在磁场中运动的总时间t=?

  （3）该半圆形磁场区域的半径R=?

 

 ①由闭合电路的欧姆定律，回路中的电流强度      ①(2分)

  两极板间的电压               ②(2分)

  对某一α粒子，在加速电场中应用动能定理得：

      ③(2分)

联立①②③解出    (1分)

    ②由题意，“粒子向上射入磁场偏转900后射出，后来又从O点返回磁场再偏转900，最后向上射出磁场．故所求

    t=T×2             ⑤(2分)

    又          ⑥(2分)

联立⑤、⑥解出     (2分)

③设α粒子在磁场中的轨迹半径为r，则

       ⑦(2分)

  由题意，    ⑧(2分)

  由⑦⑧结合，解出    (2分)

关闭