练习册

  • 练习册
  • 试题
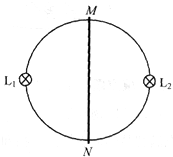
    精英家教网 > 高中物理 > 题目详情
    精英家教网如图所示，有一范围足够大的匀强磁场，磁感应强度B=0.2T，磁场方向垂直纸面向里．在磁场中有一半径r=0.4m的金属圆环，磁场与圆环面垂直，圆环上分别接有灯L1、L2，两灯的电阻均为R0=2Ω．一金属棒MN与圆环接触良好，棒与圆环的电阻均忽略不计．
    （1）若棒以v0=5m/s的速率在环上向右匀速滑动，求棒滑过圆环直径的瞬时MN中的电动势和流过灯L1的电流；
    （2）撤去金属棒MN，若此时磁场随时间均匀变化，磁感应强度的变化率为
    △B
    △t
    =
    4
    π
    T/s    ，求回路中的电动势和灯L1的电功率．
    分析：此题是电磁感应和恒定电流的综合，可用等效的思想画电路图，金属棒MN可等效为电源，把此题转化为恒定电流的题目求解即可．
    解答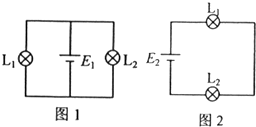：精英家教网解：（1）金属棒MN可等效为电源且无电阻，等效电路如图1所示
    MN滑过圆环直径时的电动势E1=B?2r?v0=0.8V
    MN中的电流I=
    E1
    R0/2
    =0.8A
    流过灯L1的电流I1=
    I
    2
    =0.4A
    （2）撤去金属棒MN，若此时磁场随时间均匀变化闭合电路会产生感应电流，等效电路如图2所示：
    回路中的电动势由法拉第电磁感应定律得：E2=
    △B
    △t
    ?πr2=0.64V
    回路中的电流I′=
    E2
    2R0
    =0.16A
    灯L1的电功率P1=I′2R0=5.12×10-2W
    答：（1）若棒以v0=5m/s的速率在环上向右匀速滑动，棒滑过圆环直径的瞬时MN中的电动势为0.8V和流过灯L1的电流为0.4A；
    （2）撤去金属棒MN，若此时磁场随时间均匀变化，磁感应强度的变化率为
    △B
    △t
    =
    4
    π
    T/s    ，回路中的电动势为0.64V和灯L1的电功率为5.12×10-2A．
    点评：用等效的思想画等效电路图是解题的关键，确定等效电源，用恒定电流的知识求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    如图所示,光滑水平面上有两个质量分别为m1,和m2的小球1和2,它们在一条与右侧竖直墙壁垂直的直线上前后放置.设开始时球2静止,球1以速度v0对准球2运动,不计各种摩擦,所有碰撞都足弹性的,如果要求两球只发生两次碰撞,试确定m1/m2比值的范围.

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    如图所示在厚铝板A表面中心放置一很小的放射源，向各个方向放射出质量为m、电荷量为e的β粒子，在金属网B与A板间加有竖直向上的匀强电场，电场强度为E，A、B间距离为d，B网下方有一很大的荧光屏M，M、B相距为L，荧光屏上闪光范围足一个圆，其最大半径为R，整个装置放在真空中，不计重力的影响。利用上述数据，能否用该装置测定β粒子初速度的大小?如果不能请说明理由，如果能清写出β粒子初速度大小的表达式(假设β粒子的初速度大小都相等，β粒于在穿过金属网前始终在电场中运动)。

    查看答案和解析>>

    科目：高中物理 来源：模拟题 题型：实验题

    随着全世界开始倡导低碳经济的发展，电动自行车产品已越来越受到大 家的青睐，某同学为了测定某电动自行车电池的电动势和内电阻，设计了如图1所示电路，提供的实验器材有：
    (A)电动自行车电池，电动势约为12 V，内阻未知
    (B)直流电流表量程300 mA，内阻很小
    (C)电阻箱R，阻值范围为0~999.9 Ω
    (D)定值电阻R0，标称阻值10 Ω
    (E)导线和开关
    (1)当他闭合开关时发现，无论怎样调节电阻箱，电流表都没有示数，反复检查后发现电路连接完好，估计足某一元件损坏，因此他拿来多用电表检查故障，操作如下：
    ①断开电源开关S；②将多用电表选择开关置于×1 Ω挡，调零后，红黑表笔分别接R0两端，读数为10 Ω；③将多用电表选择开关置于×10 Ω挡，调零后，将红黑表笔分别接电阻箱两端，发现指针读数如图2所示，则所测阻值为________Ω，然后又用多用电表欧姆挡对电流表进行检测，发现多用电表指针没有偏转。由以上操作可知，发生故障的元件是____________。 再更换规格相同的元件后重新连接好电路。
    (2)改变电阻箱的阻值R，分别测m阻值为R0=10 Ω的定值电阻的电流I，下列三组关于R的取值方案中，比较合理的方案是_________（选填方案编号"1"、"2"或"3"）。
    (3)根据实验数据描点，绘出的-R图象是一条直线。若直线的斜率为k，在坐标轴上的截距为b，则该电源的电动势E=________．内阻r=_______（用k、b和R0表示）。

                                                     图1                                                图2

    查看答案和解析>>

    同步练习册答案