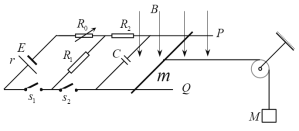
【题目】如图所示，P、Q为水平平行放置的光滑足够长金属导轨，相距L＝1m。导轨间接有E＝15V、r=1Ω的电源；0~10Ω的变阻箱R0；R1=6Ω、R2=3Ω的电阻；C=0.25F的超级电容，不计电阻的导体棒跨放在导轨上并与导轨接触良好，棒的质量为m＝0.2 kg，棒的中点用垂直棒的细绳经光滑轻质定滑轮与物体相连，物体的质量M＝0.4 kg。在导体棒ab所处区域存在磁感应强度B＝2 T方向竖直向下的匀强磁场，且范围足够大。（导轨的电阻不计，g取10 m/s2)。

（1）现闭合电键S1、S2，为了使物体保持静止，变阻箱连入电路的阻值应是多大?

（2）现断开电键S1闭合S2，待电路稳定后，求电容的带电量？

（3）使导体棒静止在导轨上，电键S2断开的情况下（电容始终正常工作）释放导体棒，试讨论物体的运动情况和电容电量的变化规律？

【答案】（1）（2） （3）

【解析】

（1）金属棒受力平衡，结合闭合电路的欧姆定律求解变阻箱连入电路的阻值；

（2）电路稳定后，分析知物体（金属棒）将做匀速运动，由法拉第电磁感应定律结合闭合电路的欧姆定律列式求解电容器两端的电压，从而求解电容器的电量；

（3）结合牛顿第二定律、电容器电量公式以及加速度的公式等讨论可知导体棒将做匀加速运动，电容器电量均匀增加.

（1）金属棒受力的方程有：

流经电阻R1的电流有：

闭合电路欧姆有：

代入数据解得：

（2）电路稳定后，分析知物体（金属棒）将做匀速运动，此时金属棒切割磁场产生电动势有：

电路端电流有：

金属棒受力力的方程有：

电容C的带电量有：

代入数据解得：

（3）物块某时受力力的方程有：

金属棒受力力的方程有：

通过金属棒的电流：

电容器时间增加的电量：

金属棒时间增加的电压：

加速度定义式：

代入数据解得： ；

即导体棒做初速度为零，加速度为2.5m/s2的匀加速直线运动，电容电量每秒均匀增加。

关闭