【题目】如图所示,质量为![]() 、半径为
、半径为![]() 的质量分布均匀的圆环静止在粗糙的水平桌面上,一质量为
的质量分布均匀的圆环静止在粗糙的水平桌面上,一质量为![]() 的光滑小球以水平速度
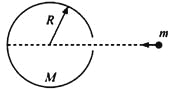
的光滑小球以水平速度![]() 通过环上的小孔正对环心射入环内,与环发生第一次碰撞后到第二次碰撞前小球恰好不会从小孔中穿出.假设小球与环内壁的碰撞为弹性碰撞,只考虑圆环与桌面之间的摩擦,且粗糙程度各处相同.求:
通过环上的小孔正对环心射入环内,与环发生第一次碰撞后到第二次碰撞前小球恰好不会从小孔中穿出.假设小球与环内壁的碰撞为弹性碰撞,只考虑圆环与桌面之间的摩擦,且粗糙程度各处相同.求:
①第一次碰撞后圆环的速度;
②第二次碰撞前圆环的位移;
③圆环通过的总位移.
【答案】①![]() ;②
;②![]() ;③
;③![]() .
.
【解析】
①设第一次刚碰撞完,小球和环各自的速度大小分别为![]() 和
和![]() ,取向左为正方向,根据动量守恒定律和机械能守恒定律,有:
,取向左为正方向,根据动量守恒定律和机械能守恒定律,有:
![]()
![]()
整理可以得到:![]() ,
,![]() .
.
②第一次碰撞后经过时间![]() ,小球恰好未从小孔中穿出,即此时二者共速,均为v1,
,小球恰好未从小孔中穿出,即此时二者共速,均为v1,
由运动学规律:![]()
对圆环,由动量定理:![]()
联立解得:![]()
假设环在第二次碰撞前已停止,其位移由动能定理:![]() 解得
解得![]()
此时小球的位移,由运动学规律:![]()
假设成立,所以在第二次碰撞前环的位移为![]()
③多次碰撞后小球和环最终静止,设圆滑受到的摩擦力为![]() ,通过的总位移为
,通过的总位移为![]() ,系统的动能全部转化为摩擦生热:
,系统的动能全部转化为摩擦生热:![]()
联立解得,圆环通过的总位移为:![]() .
.

