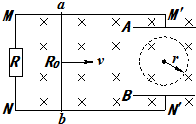
如图所示，MM′，NN′为相距L=30cm的光滑平行金属导轨，导轨左端接有定值电阻R=0.1Ω，金属导体棒ab垂直导轨放在导轨上，金属棒的电阻R0=0.3Ω，导体棒可贴着导轨无摩擦滑动，导轨电阻不计．导轨右端接一水平放置的平行板电容器，两水平金属板间的距离为d=27cm，整个装置都放在垂直纸面向里的匀强磁场中．当ab以速度v向右匀速运动时，一带电微粒刚好能以速率v在平行金属板间作半径为r=
19
m的匀速圆周运动．（g=10m/s2）求：
（l）为使带电微粒做上述要求的运动，v应为多少？
（2）若匀强磁场的磁感应强度B=2.0T，则此时作用在ab棒上的水平拉力应为多少？
分析：根据法拉第电磁感应定律表示出感应电动势，然后根据闭合电路欧姆定律求出电流，由欧姆定律求出ab两端的电压，从而表示出极板间电场强度，根据受力平衡列方程求出比荷，最后由牛顿第二定律列洛伦兹力提供向心力方程求出速度；
根据平衡条件列方程求出拉力大小．
解答：解：（1）当ab以速度v向右匀速运动时，产生的感应电动势：
E=BLv                                 
回路abNM产生的感应电流为：I=
BLv0
R+R0

则ab两端的电压（AB两板间电势差）为：Uab=IR=
BLRv
R+R0

对带电粒子：要使粒子在AB板间作匀速圆周运动，重力和电场力平衡，有：
mg=
Uab
d
q
得：
m
q
=
Uab
gd
                   
洛仑兹力提供向心力，有：qvB=m
v2
r
 
得：r=
mv
qB

联立以上五式解得：v=
(R+R0)gdr
RL

代入数据得：v=2m/s
（2）对于导体棒，做匀速运动时，拉力F等于安培力大小．
即：F=F安=BIL=
B2L2v
R+R0

代入数据得：F=1.8N
答：（l）为使带电微粒做上述要求的运动，v应为2m/s．
（2）若匀强磁场的磁感应强度B=2.0T，则此时作用在ab棒上的水平拉力应为1.8N．
点评：解决此类问题时一定要注意ab两点间的电压为路端电压，不是感应电动势大小也不是内电压．
关闭