 (1)用氦氖激光器进行双缝干涉实验,已知所用双缝间的距离为d=0.1mm,双缝到屏的距离为L=6.0m,测得屏上干涉条纹中相邻明条纹的间距是3.8cm,氦氖激光器发出的红光的波长是
(1)用氦氖激光器进行双缝干涉实验,已知所用双缝间的距离为d=0.1mm,双缝到屏的距离为L=6.0m,测得屏上干涉条纹中相邻明条纹的间距是3.8cm,氦氖激光器发出的红光的波长是6.33×10-7
6.33×10-7
m;假如把整个干涉装置放入折射率为| 4 | 3 |
2.85
2.85
cm.(结果保留三位有效数字)(2)如图所示,是一列简谐横波在某一时刻的波形图象,已知该波沿x轴正方向传播,波速为5m/s,求:
①该波的波长和周期;
②P质点从该时刻起第一次到达正的最大位移处所用的时间;
③画出波从此时刻起再传播1.5个波长时的波形图.
分析:(1)根据双缝干涉的条纹间距公式求出红光的波长.光从空气进入水,频率不变,根据波速、频率、波长的关系得出波长的变化,从而求出条纹的间距变化.
(2)相邻两个波峰(或波谷)间的距离等于波长,根据波长和波速求出波的周期.
P质点从该时刻起第一次到达正的最大位移处所用的时间等于左边相邻的波峰传播到4.5m处所需的时间,根据波形传播的距离和波速求出传播所需的时间.
波从此时刻起再传播1.5个波长时的波形图,根据传播的周期性,知与传播半个周期后的波形图相同.
(2)相邻两个波峰(或波谷)间的距离等于波长,根据波长和波速求出波的周期.
P质点从该时刻起第一次到达正的最大位移处所用的时间等于左边相邻的波峰传播到4.5m处所需的时间,根据波形传播的距离和波速求出传播所需的时间.
波从此时刻起再传播1.5个波长时的波形图,根据传播的周期性,知与传播半个周期后的波形图相同.
解答:解:(1)在双缝干涉中,相邻的亮条纹的间距△x=
λ
所以红光的波长是λ=
≈6.33×10-7m
红光从空气进入水中,频率不变,f=
=
在水中光速v=
故红光在水中的波长λ′=
所以在水中,相邻明条纹的间距△x′=
=2.85cm.
故答案为:6.33×10-7,2.85.
(2)①由题图知,该波波长为λ=4m,周期T=
=0.8s.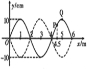
②P点第一次到达最高点的时间t=
=
s=0.7s.
③波传播1.5个波长与经过二分之一个周期后的波形图相同,如图中虚线所示.
答:①波长和周期分别为4m,0.8s.
②P质点从该时刻起第一次到达正的最大位移处所用的时间为0.7s.
③波形图如图所示.
| L |
| d |
所以红光的波长是λ=
| △x•d |
| L |
红光从空气进入水中,频率不变,f=
| c |
| λ |
| v |
| λ′ |
在水中光速v=
| c |
| n |
故红光在水中的波长λ′=
| λ |
| n |
所以在水中,相邻明条纹的间距△x′=
| △x |
| n |
故答案为:6.33×10-7,2.85.
(2)①由题图知,该波波长为λ=4m,周期T=
| λ |
| v |

②P点第一次到达最高点的时间t=
| 4.5-1 |
| 5 |
| 3.5 |
| 5 |
③波传播1.5个波长与经过二分之一个周期后的波形图相同,如图中虚线所示.
答:①波长和周期分别为4m,0.8s.
②P质点从该时刻起第一次到达正的最大位移处所用的时间为0.7s.
③波形图如图所示.
点评:解决本题的关键知道光从空气进入水中频率不变,掌握双缝干涉条纹的间距公式.以及知道波长、波速、频率的关系.

