搜索
两个所受重力大小分别为GA和GB的小球A和B，用轻杆连接，放置在光滑的半球形碗内．小球A、B与碗的球心O在同一竖直平面内，如图所示，若碗的半径为R，细杆的长度为| 2 |
arctan
| GA+GB |
| GA-GB |
arctan
．| GA+GB |
| GA-GB |
分析：先对球A受力分析，受重力、拉力和支持力；再对球B受力分析，受重力、拉力和支持力；然后根据共点力平衡条件列式，求出角度θ．
解答：解：细杆的长度为
R，故球与圆心的连线与细杆的夹角为45°；
取杆方向为x轴，与杆垂直为y轴，对A受力分析，受重力GA、拉力F和支持力FN1，如图
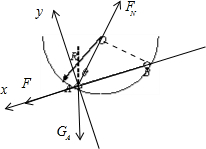
根据共点力平衡条件，有
x方向：F+GAcosθ=FN1cos45°
y方向：GAsinθ=FN1sin45°
整理得：F+GAcosθ=GAsinθ
对B，同理得：F=GBcosθ+GBsinθ
解得：tanθ=
故θ=arctan
故答案为：arctan
| 2 |
取杆方向为x轴，与杆垂直为y轴，对A受力分析，受重力GA、拉力F和支持力FN1，如图
根据共点力平衡条件，有
x方向：F+GAcosθ=FN1cos45°
y方向：GAsinθ=FN1sin45°
整理得：F+GAcosθ=GAsinθ
对B，同理得：F=GBcosθ+GBsinθ
解得：tanθ=
| GA+GB |
| GA-GB |
故θ=arctan
| GA+GB |
| GA-GB |
故答案为：arctan
| GA+GB |
| GA-GB |
点评：本题关键是对两个小球受力分析，然后根据共点力平衡条件列方程求解．．
