练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
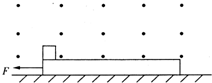
    如图，空间有一垂直纸面的磁感应强度为0.5T的匀强磁场，一质量为0.2kg，且足够长的绝缘木板静止在光滑水平面上，在木板左端静置一质量0.1kg，电荷量为+0.2C的滑块，滑块与绝缘木板之间的动摩擦因数为0.5，滑块受到的最大静摩擦力可认为等于滑动摩擦力，现对木板施加方向水平向左，大小为0.6N的恒力，g取10m/s2，则最终木板做匀加速运动的加速度为
    3m/s2
    3m/s2
    ，滑块做匀速直线运动的速度为
    10 m/s
    10 m/s
    ．
    分析：先求出木块静摩擦力能提供的最大加速度，再根据牛顿第二定律判断当0.6N的恒力作用于木板时，系统一起运动的加速度，当滑块获得向左运动的速度以后又产生一个方向向上的洛伦兹力，当洛伦兹力等于重力时滑块与木板之间的弹力为零，此时摩擦力等于零，此后物块做匀速运动，木板做匀加速直线运动．
    解答：解：由于动摩擦因数为0.5，静摩擦力能提供的最大加速度为5m/s2，所以当0.6N的恒力作用于木板时，系统一起以a=
    F
    M+m
    =
    0.6
    0.2+0.1
    =2m/s2的加速度一起运动，当滑块获得向左运动的速度以后又产生一个方向向上的洛伦兹力，当洛伦兹力等于重力时滑块与木板之间的弹力为零，此时Bqv=mg，解得：v=10m/s，此时摩擦力消失，滑块做匀速运动，而木板在恒力作用下做匀加速运动，a=
    F
    m
    =
    0.6
    0.2
    =3m/s2
    故答案为：3 m/s2，10 m/s
    点评：本题主要考查了牛顿第二定律的直接应用，要求同学们能正确分析木板和滑块的受力情况，进而判断运动情况．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    如图，空间某区域中有一匀强磁场，磁感应强度方向水平，且垂直于纸面向里，磁场上边界b 和下边界d水平．在竖直面内有一矩形金属统一加线圈，线圈上下边的距离很短，下边水平．线圈从水平面a开始下落．已知磁场上下边界之间的距离大于水平面a、b之间的距离．若线圈下边刚通过水平面b、c（位于磁场中）和d时，线圈所受到的磁场力的大小分别为Fb、Fc和Fd，则（　　）

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    （2013?淄博一模）如图，空间区域Ⅰ中存在着水平向右的匀强电场，电场强度为E，边界MN垂直于该电场．MN右侧有一以O为圆心的圆形匀强磁场区域Ⅱ，磁场方向垂直纸面向外，磁感应强度为B．在圆形磁场区域的正下方有一宽度为L的显示屏CD，显示屏的水平边界C、D两点到O点的距离均为L．质量为m、带电量为+q的粒子，从A点由静止释放，经电场加速后，沿AO方向进入磁场，恰好打在显示屏上的左边界C点．已知A点到MN的距离为s，不计粒子重力，求

    （1）粒子在磁场中的轨道半径r；
    （2）圆形磁场的半径R；
    （3）改变释放点A的位置，使从A点释放的粒子仍能沿AO方向进入磁场且都能打在显示屏上时，释放点A到MN的距离范围．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    （2009?河西区模拟）B组：空间存在一匀强磁场B，其方向垂直纸面向里，另有一个点电荷+Q的电场，如图所示，一带电-q的粒子以初速度v0从某处垂直电场、磁场入射，初位置到点电荷的距离为r，则粒子在电磁场中的运动轨迹可能为（　　）

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    （2010?海南模拟）如图所示，某空间有一竖直向下的匀强电场，电场强度E=1.0×102V/m，一块足够大的接地金属板水平放置在匀强电场中，在金属板的正上方高度h=0.80m的C处有一粒子源，可在纸面内向水平线以下的各个方向均匀放出带电粒子，带电粒子的初速度v0=2.0×102m/s，质量为m=2.0×10-15kg，电荷量为q=+10-12C，粒子最终落在金属板上．若不计粒子重力，求：
    （1）粒子源所在处C点的电势；
    （2）带电粒子打在金属板上时的动能；
    （3）若只将电场换为匀强磁场，磁场分布在半径为h，圆心在C点的圆形区域内，磁场方向垂直纸面向里，磁感应强度为B=0.5T，从粒子源射出的粒子打在金属板上的范围．（结果保留两位有效数字，
    		3
    =1.73    ）

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    精英家教网如图所示，空间有一理想边界 MN 将方向相反的匀强磁场分为上下两部分，边界以上的磁场方向垂直纸面向里，磁感应强度大小为 B1，边界以下的磁场方向垂直纸面向外，磁感应强度大小为 B2，且 B1＞B2．将一根电阻为 R 的金属导线制成弧度为90°的扇形闭合线框 Oab．开始时，线框处于图中所示位置，现使线框绕垂直于纸面的 轴 O 以恒定角速度ω 在纸面内顺时针转动．设线框内沿逆时针方向为电流的正方向，下列能正确表示导线框内电流随时间变化的是（　　）

    查看答案和解析>>

    同步练习册答案