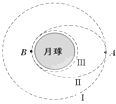
【题目】如图所示,在“嫦娥”探月工程中,设月球半径为R,月球表面的重力加速度为g0。飞船在半径为4R的圆形轨道Ⅰ上运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时,再次点火进入近月轨道Ⅲ绕月做圆周运动,则( )
A.飞船在轨道Ⅰ、Ⅲ上运行的周期之比为81
B.飞船在轨道Ⅲ的运行速率大于![]()
C.飞船在轨道Ⅰ上经过A处的加速度小于在轨道Ⅱ上经过A处的加速度
D.飞船在轨道Ⅰ上经过A处的运行速率小于飞船在轨道Ⅱ上经过A处的运行速率
【答案】A
【解析】
A.根据开普勒第三定律
![]()
![]()
其中
![]()
解得
![]()
故A正确;
B.设月球的质量为M,飞船的质量为m,飞船绕月运动速度为v,由万有引力提供向心力
![]()
![]()
解得![]() ,故B错误;
,故B错误;
C.由万有引力提供向心力
![]()
飞船在轨道Ⅰ上经过A处的加速度等于在轨道Ⅱ上经过A处的加速度,故C错误;
D.飞船在轨道Ⅰ上的A处减速做向心运动进入轨道Ⅱ,飞船在轨道Ⅰ上经过A处的运行速率大于飞船在轨道Ⅱ上经过A处的运行速率,故D错误。
故选A。

