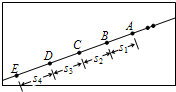
 (2006•松江区二模)一小球沿光滑斜面向下运动,用每隔0.1s曝光一次的频闪照相机拍摄下不同时刻小球的位置照片如图所示,选小球的五个连续位置A、B、C、D、E进行测量,测得距离s1、s2、s3、s4的数据如表格所示.
(2006•松江区二模)一小球沿光滑斜面向下运动,用每隔0.1s曝光一次的频闪照相机拍摄下不同时刻小球的位置照片如图所示,选小球的五个连续位置A、B、C、D、E进行测量,测得距离s1、s2、s3、s4的数据如表格所示.| s1(cm) | s2(cm) | s3(cm) | s4(cm) |
| 8.20 | 9.30 | 10.40 | 11.50 |
1.1
1.1
m/s2.(2)根据以上数据能否求出斜面的倾角?
能
能
(填能或不能,重力加速度g为已知)(3)根据以上数据可知小球在位置A的速度是
0.765
0.765
m/s.分析:(1)根据匀变速直线运动在连续相等时间内的位移之差是一恒量求出小球的加速度;
(2)通过加速度,根据牛顿第二定律求出斜面的倾角;
(3)根据某段时间内的平均速度等于中间时刻的瞬时速度,根据该规律求出B点的速度,根据速度时间公式求出A的速度.
(2)通过加速度,根据牛顿第二定律求出斜面的倾角;
(3)根据某段时间内的平均速度等于中间时刻的瞬时速度,根据该规律求出B点的速度,根据速度时间公式求出A的速度.
解答:解:(1)根据△x=aT2,解得a=
=
m/s2=1.10m/s2;
(2)能.根据牛顿第二定律得,a=
=gsinθ;
则sinθ=
.因为a与g已知,则可以求出斜面的倾角;
(3)vB=
=
m/s=0.875m/s.
则vA=vB-aT=0.875-1.10×0.1m/s=0.765m/s.
故答案为:(1)1.1;能;0.765.
| △x |
| T2 |
| 1.10×10-2 |
| 0.01 |
(2)能.根据牛顿第二定律得,a=
| Gsinθ |
| m |
则sinθ=
| a |
| g |
(3)vB=
| S1+S2 |
| 2T |
| (8.20+9.30)×10-2 |
| 2×0.1 |
则vA=vB-aT=0.875-1.10×0.1m/s=0.765m/s.
故答案为:(1)1.1;能;0.765.
点评:解决本题的关键掌握匀变速直线运动的推论,并能灵活运用.

