如图所示，用两根轻绳和一根轻弹簧将质量均为m的A、B两小球以及水平天花板上的固定点O之间两两连接，然后用一水平方向的力F作用于A球上，此时两根轻绳均处于直线状态，且OB绳恰好处于竖直方向，两球均处于静止状态，已知三段长度之比为OA：AB：OB=3：4：5．试确定：
（1）弹簧OA的拉力．
（2）若突然将F撤去，则撤去瞬间，小球A的加速度．
分析：（1）由题，OB恰好处于竖直方向，说明轻绳AB对B球没有拉力，对A进行受力分析，由平衡条件求出弹簧OA的拉力．
（2）若突然将F撤去，弹簧的拉力没有变化，由牛顿第二定律求出此瞬间小球A的加速度．
解答：解：（1）已知三段长度之比为OA：AB：OB=3：4：5，所以∠AOB=53°．由几何知识得到，由题意，OB恰好处于竖直方向，说明轻绳AB对B球没有拉力，则A球受到重力mg、水平力F和弹簧OA的拉力T，如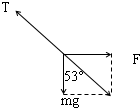图，根据平衡条件得：
T=
mg
cos53°
=
5
3
mg
（2）突然将F撤去的瞬间，弹簧的弹力没有来得及变化，则小球A所受的合力大小与F大小相等，即：F合=F=mgtan53°=ma
得：a=
F
m
=
4
3
g，方向水平向左．
答：（1）弹簧OA的拉力为
5
3
mg．
（2）若突然将F撤去，则撤去瞬间，小球A的加速度是
4
3
g．
点评：本题物体先处于平衡状态，由平衡条件求解弹簧的拉力和F；撤去F后小球处于非平衡状态，由牛顿第二定律求解小球瞬时的加速度，关键抓住弹簧的弹力不能突变的特点分析瞬间小球的合力．
关闭