利用图1所示的装置可测量滑块在斜面上运动的加速度.一斜面上安装有两个光电门,其中光电门乙固定在斜面上靠近底端处,光电门甲的位置可移动,当一带有遮光片的滑块自斜面上滑下时,与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间t.改变光电门甲的位置进行多次测量,每次都使滑块从同一点由静止开始下滑,并用米尺测量甲、乙之间的距离s,记下相应的t值;所得数据如下表所示.

完成填空和作图:
(1)若滑块所受摩擦力为一常量,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量之间所满足的关系式是s=
(2)根据表中给出的数据,在图2给出的坐标纸上画出s/t-t图线;
(3)由所画出的s/t-t图线,得出滑块加速度的大小为a=

| s(m) | 0.500 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
| t(ms) | 292.9 | 371.5 | 452.3 | 552.8 | 673.8 | 776.4 |
| s/t(m/s) | 1.71 | 1.62 | 1.55 | 1.45 | 1.34 | 1.22 |
(1)若滑块所受摩擦力为一常量,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量之间所满足的关系式是s=
s=v1t-
at2
| 1 |
| 2 |
s=v1t-
at2
;| 1 |
| 2 |
(2)根据表中给出的数据,在图2给出的坐标纸上画出s/t-t图线;
(3)由所画出的s/t-t图线,得出滑块加速度的大小为a=
2.0
2.0
m/s2(保留2位有效数字).分析:可以把光电门甲至乙的匀加速运动看成反向的匀减速运动,写出测量值s和t四个物理量之间所满足的关系式.
由位移时间关系式整理得到
-t图线的表达式,并找出图线的斜率和加速度关系.
由位移时间关系式整理得到
| s |
| t |
解答: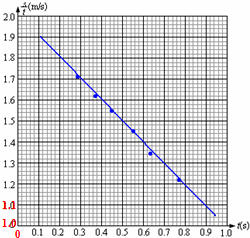 解:(1)已知滑块沿斜面下滑时做匀加速运动,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量.因为时速度v1是下滑的末速度,所以我们可以看下滑的逆过程,所以满足的关系式是:s=v1t-
解:(1)已知滑块沿斜面下滑时做匀加速运动,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量.因为时速度v1是下滑的末速度,所以我们可以看下滑的逆过程,所以满足的关系式是:s=v1t-
at2
(2)见下图
(3)由s=v1t-
at2得
=v1-
at
作图求出斜率k=-0.9897m/s2,a=2|k|≈2.0m/s2
(1)s=v1t-
at2(2)如图(3)2.0
 解:(1)已知滑块沿斜面下滑时做匀加速运动,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量.因为时速度v1是下滑的末速度,所以我们可以看下滑的逆过程,所以满足的关系式是:s=v1t-
解:(1)已知滑块沿斜面下滑时做匀加速运动,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v1、测量值s和t四个物理量.因为时速度v1是下滑的末速度,所以我们可以看下滑的逆过程,所以满足的关系式是:s=v1t-| 1 |
| 2 |
(2)见下图
(3)由s=v1t-
| 1 |
| 2 |
| s |
| t |
| 1 |
| 2 |
作图求出斜率k=-0.9897m/s2,a=2|k|≈2.0m/s2
(1)s=v1t-
| 1 |
| 2 |
点评:题目的难度在于:物体加速下滑时,我们研究了它的逆过程,并且要整理图象所要求的表达式.

