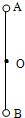如图所示，长为2L的轻杆，两端各固定一小球，A球质量为m1，B球质量为m2，且m1＞m2，过杆的中点O有一水平光滑固定轴，杆可在不同的初始条件下绕轴在竖直平面内转动．下列说法中正确的是（　　）
分析：杆模型在最高点的最小速度可以为零，当杆子对轴的作用力为零时，知B球对杆的作用力和A球对杆的作用力大小相等，方向相反，根据牛顿第二定律求出杆子的角速度．
解答：解：A、杆模型A球到最高点的速度可以为零．当A球速度为零时，B球速度也为零．故A正确，B错误．
C、在最低点有：F2-m2g=m2Lω2，解得F2=m2g+m2Lω2．在最高点，有：F1+m1g=mLω2，解得F1=mLω2-m1g．则F1=F2，解得ω=
(m1+m2)g
(m1-m2)L
．故C正确．
D、在图示位置，B球的最小速度为零，则最小拉力为m2g．故D错误．
故选AC．
点评：解决本题的关键搞清小球做圆周运动向心力的来源，运用牛顿第二定律进行分析．
关闭