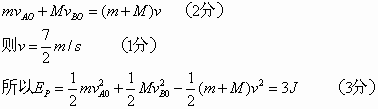如图所示，质量为M＝6 kg的滑板B静止在光滑水平面上，滑板的右端固定一轻弹簧．在滑板的最左端放一可视为质点的小物体A，弹簧的自由端C与A相距L＝1 m．弹簧下面的那段滑板是光滑的，C左侧的那段滑板是粗糙的，物体A与这段粗糙滑板间的动摩擦因数为μ＝0.2，A的质量m＝2 kg．滑板受到水平向左恒力F作用1 s后撤去，撤去水平力F时A刚好滑到C处，g取10 m/s2，

求：(1)撤去恒力F作用时小物体A的和滑板的速度各为多大？

(2)A压缩弹簧过程中弹簧的最大弹性势能EP；

(3)试通过计算说明撤去F后，小物体能否与滑板相分离？若能，分离后物体和滑板的速度各为多大？若不能，小物体将停止在滑板上的什么位置？

答案：
解析：

　　解：(1)在这1 s内滑板B和小物体A均向左做匀加速运动，对A有：　　(1分)

　　　　(1分)

　　这1 s内滑板B的位移为：　　(1分)

　　

　　撤去水平力F时，A、B的速度

　　(2)当A、B速度相等时弹簧的弹性势能最大，根据动量守恒有

　　

　　(3)撤去F后，当弹簧恢复原长过程中，设小物体没有滑出滑板，且共同速度为v/，相对位移为s

　　A、B动量　　(1分)

　　解得v／＝3.5 m/s　　(1分)

　　能量守恒　　(2分)

　　解得s＝0.75 m＜1 m，　　(1分)

　　即小物体没有滑出滑板，两者不会分离，小物体将停在距C　0.75 m处．　　(2分)


关闭