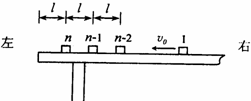
精英家教网如图所示，n个相同的木块（可视为质点），每块的质量都是m，从右向左沿同一直线排列在水平桌面上，相邻木块间的距离均为l，第n个木块到桌边的距离也是l，木块与桌面间的动摩擦因数为μ．开始时，第1个木块以初速度υ0向左滑行，其余所有木块都静止，在每次碰撞后，发生碰撞的木块都粘在一起运动．最后第n个木块刚好滑到桌边而没有掉下．
（1）求在整个过程中因碰撞而损失的总动能．
（2）求第i次（i≤n一1）碰撞中损失的动能与碰撞前动能之比．
（3）若n=4，l=0.10m，υ0=3.0m/s，重力加速度g=10m/s2，求μ的数值．
分析：（1）在整个过程中因碰撞和摩擦损失的总动能等于初动能△Ek=
1
2
m
v
2
0
，求出克服摩擦力做功，得到因摩擦而损失的动能，就能求得因碰撞而损失的总动能．
（2）根据动量守恒定律求出第i次（i≤n一1）碰撞前后速度关系，即可求得碰撞中损失的动能与碰撞前动能之比．
（3）分别求得各次碰撞前后的动能，得到第3次碰撞后的动能，结合题意：第n=4个木块刚好滑到桌边而没有掉下，运用功能关系求μ．
解答：解：（1）整个过程木块克服摩擦力做功
   W=μmgl+μmg•2l+…+μmg•nl=
n(n+1)μmgl
2
    ①
根据功能关系，整个过程中由于碰撞而损失的总动能为
△Ek=Ek0-W      ②
得△Ek=
1
2
m
v
2
0
-
n(n+1)μmgl
2
       ③
（2）设第i次（i≤n一1）碰撞前木块的速度为υi，碰撞后速度为υi′，则
（i+1）mυi′=imυi ④
碰撞中损失的动能△E时与碰撞前动能Eki之比为
  
△EKi
EKi
=
1
2
im
υ
2
i
-
1
2
(i+1)m
υ
．•2
i
1
2
im
υ
2
i
（i≤n-1）⑤
解得
△EKi
EKi
=
1
i+1
（i≤n-1）⑥
（3）初动能Ek0=
1
2
m
v
2
0

第1次碰撞前
E
  
K1
=EK0-μmgl              ⑦
第1次碰撞后   EK1′=EK1-△EK1=EK1-
1
2
EK1=
1
2
EK0-
1
2
μmgl   ⑧
第2次碰撞前  EK2=EK1′=μ（2mg）l=
1
2
EK0-
1
2
μmgl
第2次碰撞后 EK2′=EK2-△EK2=
1
3
EK0-
5
3
μmgl
第3次碰撞前   EK3=EK3′-μ（3mg）l=
1
3
EK0-
14
3
μmgl
第3次碰撞后   EK3′=EK3-△EK3=
1
4
EK0-
7
2
μmgl
据题意有    
1
4
EK0-
7
2
μmgl=μ（4mg）l      ⑨
代入数据，联立求解得    μ=0.15         ⑩
答：
（1）在整个过程中因碰撞而损失的总动能为
1
2
m
v
2
0
-
n(n+1)μmgl
2
．
（2）第i次（i≤n一1）碰撞中损失的动能与碰撞前动能之比为1：（i+1）．
（3）若n=4，l=0.10m，υ0=3.0m/s，重力加速度g=10m/s2，μ的数值是0.15．
点评：本题是动量守恒与功能关系结合的类型，采用归纳法求解若干次碰撞的过程，难度较大．
关闭