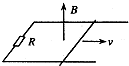
 如图所示,间距为L、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m、电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中.现使金属棒以初速度v沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )
如图所示,间距为L、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m、电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中.现使金属棒以初速度v沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )分析:对金属棒进行受力分析,求出金属棒受到的合外力,然后判断金属棒的运动性质;
由动能定理求出克服安培力所做的功;
求出感应电荷量的表达式,然后求出金属棒的位移;
由能量守恒定律和串联电路的特点求出电阻R上产生的焦耳热.
由动能定理求出克服安培力所做的功;
求出感应电荷量的表达式,然后求出金属棒的位移;
由能量守恒定律和串联电路的特点求出电阻R上产生的焦耳热.
解答:解:金属棒在整个运动过程中,受到竖直向下的重力,竖直向上的支持力,这两个力合力为零,受到水平向左的安培力,金属棒受到的合力为安培力;
A、金属棒受到的安培力F=BIL=BL
=BL
=
,金属棒受到安培力作用而做减速运动,速度v不断减小,安培力不断减小,加速度不断减小,故金属棒做加速度逐渐减小的变减速运动,故A错误;
B、整个过程中由动能定理可得:-W安=0-
mv2,金属棒克服安培力做功为W安=
mv2,故B正确;
C、整个过程中感应电荷量q=I△t=
△t,又E=
=
,
联立得 q=
故金属棒的位移s=
,故C正确;
D、克服安培力做功把金属棒的动能转化为焦耳热,由于金属棒电阻与电阻串联在电路中,且阻值相等,则电阻R上产生的焦耳热Q=
W安=
mv2,故D错误;
故选BC.
A、金属棒受到的安培力F=BIL=BL
| E |
| 2R |
| BLv |
| 2R |
| B2L2v |
| 2R |
B、整个过程中由动能定理可得:-W安=0-
| 1 |
| 2 |
| 1 |
| 2 |
C、整个过程中感应电荷量q=I△t=
| E |
| 2R |
| △Φ |
| △t |
| BLs |
| △t |
联立得 q=
| BLs |
| 2R |
故金属棒的位移s=
| 2qR |
| BL |
D、克服安培力做功把金属棒的动能转化为焦耳热,由于金属棒电阻与电阻串联在电路中,且阻值相等,则电阻R上产生的焦耳热Q=
| 1 |
| 2 |
| 1 |
| 4 |
故选BC.
点评:金属棒在运动过程中克服安培力做功,把金属棒的动能转化为焦耳热,在此过程中金属棒做加速度减小的减速运动;对棒进行受力分析、熟练应用法拉第电磁感应定律、欧姆定律、动能定理等正确解题.

