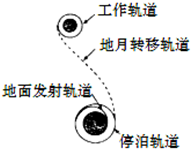
如图为我国发射的“嫦娥一号”探月卫星简化后的运行路线示意图．卫星由地面发射后，经过发射轨道进入停泊轨道，然后在停泊轨道上经过调速后进入地月转移轨道，再次调速后进入工作轨道，卫星开始对月球进行探测．已知地球与月球的质量之比为a，卫星的停泊轨道与工作轨道的半径之比为b，卫星在停泊轨道和工作轨道上均可视为做匀速圆周运动，则卫星（　　）
分析：根据万有引力提供向心力得出线速度、周期与中心天体质量和轨道半径的关系，从而得出速度和周期之比．第一宇宙速度的轨道半径等于地球的半径，结合轨道半径的大小比较速度大小．
解答：解：A、根据G
Mm
r2
=m
v2
r
得，v=
GM
r
，则在停泊轨道和工作轨道上的速度之比为
v1
v2
=
a
b
．故A正确．
B、根据G
Mm
r2
=mr
4π2
T2
得，T=
4π2r3
GM
，则在停泊轨道和工作轨道上的周期之比为
T1
T2
=
b3
a
．故B错误．
C、第一宇宙速度的轨道半径等于地球的半径，根据v=
GM
r
，知在停泊轨道上运行的速度小于地球的第一宇宙速度．故C错误．
D、沿地月转移轨道运动的过程中，地球、月球对它的万有引力的合力先做负功，再做正功．故D错误．
故选：A．
点评：解决本题的关键掌握万有引力提供向心力这一理论，知道线速度、周期与轨道半径的关系．
关闭