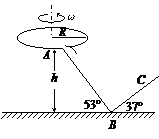
如图所示，一水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，经光滑的过渡圆管进入轨道ABC。以知AB段斜面倾角为53°，BC段斜面倾角为37°，滑块与圆盘及斜面间的动摩擦因数均μ=0.5 ，A点离B点所在水平面的高度h=1.2m。滑块在运动过程中始终未脱离轨道，不计在过渡圆管处和B点的机械能损失，最大静摩擦力近似等于滑动摩擦力，取g=10m/s2，sin37°=0.6; cos37°=0.8

（1）若圆盘半径R=0.2m，当圆盘的角速度多大时，滑块从圆盘上滑落？

（2）若取圆盘所在平面为零势能面，求滑块到达B点时的机械能。

（3）从滑块到达B点时起，经0.6s正好通过C点，求BC之间的距离。

⑴μmg=mω2R，ω=5rad/s(2) 4m/s(3)0.76m


解析:

⑴μmg=mω2R，ω=5rad/s

⑵滑块在A点时的速度vA=ωR=1m/s，A到B过程用动能定理：

mgh-μmgcos53°·h/sin53°=

在B点时的机械能EB=-mgh=-4J，此时B的速度为4m/s

⑶滑块在B点时的速度：vB=4m/s。滑块上运动时加速度大小a1=g(sin37°+μcos37°)=10m/s2

返回时的加速度大小：

a2=g(sin37°-μcos37°)=2m/s2，

因此BC间的距离：

sBC==0.76m，

就是说上滑后又下滑，但加速度是不一样的。   

关闭