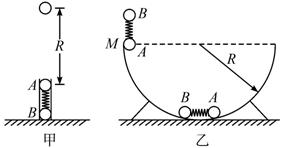
质量均为m的两小球A、B间有压缩的轻、短弹簧，弹簧处于锁定状态，两球的大小尺寸和弹簧尺寸都可忽略，把它们放入固定在水平面上的竖直光滑发射管内，解除弹簧锁定后，B球仍然保持静止，A球能上升的最大高度为R，如图(甲)所示。现在让两球(包括同样锁定的弹簧)沿光滑的半径也为R的固定半圆槽左端的M点由静止开始滑下，如图(乙)所示，到达半圆槽的最低点时解除弹簧锁定，求A球离开半圆槽后能上升的最大高度。

1.9 R

解析：解除锁定后弹簧将弹性势能全部转化为A球的机械能，则弹簧的弹性势能为E弹＝mgR

AB系统由水平位置滑到圆轨道最低点时速度为v0，由机械能守恒定律，有

2mgR＝2/2

解除弹簧锁定后，弹簧恢复到原长时，A、B的速度分别为va、vb，由动量守恒和能量守恒，则有

2mv0＝mva＋mvb

2/2＋E弹＝mv2a/2＋mv2b/2

解得：va＝－(不符合题意，舍去)

va＝＋

设A球相对半圆槽口上升的最大高度为h，则

mg(h＋R)＝mv2a

解得：h＝(＋)R≈1.9 R。

关闭