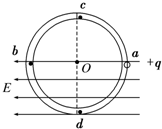
 如图所示,一个内壁光滑的环形塑料管竖直放置,ab为该环形塑料管水平直径,其长度为2R,ab及其以下部分处于水平向左的匀强电场中,电场强度为E.现将一质量为m、带电荷量为+q的小球从管中a点由静止释放,球的直径略小于管的内径,已知qE=mg,求:
如图所示,一个内壁光滑的环形塑料管竖直放置,ab为该环形塑料管水平直径,其长度为2R,ab及其以下部分处于水平向左的匀强电场中,电场强度为E.现将一质量为m、带电荷量为+q的小球从管中a点由静止释放,球的直径略小于管的内径,已知qE=mg,求:(1)小球第一次经过b点时的速度;
(2)小球第一次经过c点时对管壁的压力;
(3)小球第一次经过adb过程中对管道的最大压力.
分析:(1)小球从a运动到b的过程中,重力和电场力做功,根据动能定理求解小球第一次经过b点时的速度;
(2)由动能定理求出小球到达c点的速度,根据牛顿第二定律求解小球第一次经过c点时对管壁的压力;
(3)根据动能定理得到速度与图中夹角θ的表达式,由数学知识求出速度的最大值,此时小球对管道的最大压力.根据牛顿第二定律求出最大压力.
(2)由动能定理求出小球到达c点的速度,根据牛顿第二定律求解小球第一次经过c点时对管壁的压力;
(3)根据动能定理得到速度与图中夹角θ的表达式,由数学知识求出速度的最大值,此时小球对管道的最大压力.根据牛顿第二定律求出最大压力.
解答:解:(1)小球从a运动到b的过程中,由动能定理得
(2)小球从a运动到c的过程中,由动能定理
-mgR+EqR=
m
已知qE=mg,得vC=0
在c点,mg+FN=m
联立解得,FN=-mg,即轨道对小球的支持力竖直向上,则根据牛顿第三定律得:小球第一次经过c点时对管壁的压力大小为mg,方向竖直向下.
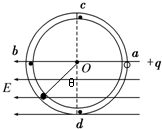
(3)设当小球在如图夹角θ时速度最大,由动能定理
(R+Rsinθ)Eq+mgRcosθ=
mv2
得2gR(1+sinθ+cosθ)=v2
所以v=
=
当θ=45°时 最大速度为v=
此时重力与电场力的合力为
mg
根据牛顿第二定律得:FN-mg=m
得 FN=
mg+m
=
mg+m
=mg(2+3
)
故小球第一次经过adb过程中对管道的最大压力是mg(2+3
)
答:(1)小球第一次经过b点时的速度是2
;
(2)小球第一次经过c点时对管壁的压力大小为mg,方向竖直向下;
(3)小球第一次经过adb过程中对管道的最大压力是mg(2+3
).
|

(2)小球从a运动到c的过程中,由动能定理
-mgR+EqR=
| 1 |
| 2 |
| v | 2 C |
已知qE=mg,得vC=0
在c点,mg+FN=m
| ||
| R |
联立解得,FN=-mg,即轨道对小球的支持力竖直向上,则根据牛顿第三定律得:小球第一次经过c点时对管壁的压力大小为mg,方向竖直向下.
(3)设当小球在如图夹角θ时速度最大,由动能定理
(R+Rsinθ)Eq+mgRcosθ=
| 1 |
| 2 |
得2gR(1+sinθ+cosθ)=v2
所以v=
| 2gR(1+sinθ+cosθ) |
2gR[1+
|
当θ=45°时 最大速度为v=
2gR(1+
|
此时重力与电场力的合力为
| 2 |
根据牛顿第二定律得:FN-mg=m
| v2 |
| R |
得 FN=
| 2 |
| v2 |
| R |
| 2 |
2gR(1+
| ||
| R |
| 2 |
故小球第一次经过adb过程中对管道的最大压力是mg(2+3
| 2 |
答:(1)小球第一次经过b点时的速度是2
| gR |
(2)小球第一次经过c点时对管壁的压力大小为mg,方向竖直向下;
(3)小球第一次经过adb过程中对管道的最大压力是mg(2+3
| 2 |
点评:本题关键要分析求出小球的运动,然后多次根据动能定理、向心力公式和牛顿第二定律列式求解.

