航天飞机,可将物资运送到空间站,也可维修空间站出现的故障.
(1)若已知地球半径为R,地球表面重力加速度为g,某次维修作业中,与空间站对接的航天飞机的速度计显示飞机的速度为v,则该空间站轨道半径R′为多大?
(2)为完成某种空间探测任务,在空间站上发射的探测器通过向后喷气而获得反冲力使其启动.已知探测器的质量为M,每秒钟喷出的气体质量为m,为了简化问题,设喷射时探测器对气体做功的功率恒为P,在不长的时间 内探测器的质量变化较小,可以忽略不计.求喷气t秒后探测器获得的动能是多少?
(1)若已知地球半径为R,地球表面重力加速度为g,某次维修作业中,与空间站对接的航天飞机的速度计显示飞机的速度为v,则该空间站轨道半径R′为多大?
(2)为完成某种空间探测任务,在空间站上发射的探测器通过向后喷气而获得反冲力使其启动.已知探测器的质量为M,每秒钟喷出的气体质量为m,为了简化问题,设喷射时探测器对气体做功的功率恒为P,在不长的时间 内探测器的质量变化较小,可以忽略不计.求喷气t秒后探测器获得的动能是多少?
【答案】分析:(1)根据地球表面重力加速度公式和万有引力等于向心力联立求解出空间站的轨道半径;
(2)对t秒内喷出的气体运用动能定理求出喷气速度,再根据动量守恒定律求出探测器的速度,进一步求出探测器的动能.
解答:解:(1)设地球质量为M,在地球表面
g=G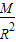
设空间站质量为m′绕地球作匀速圆周运动时
G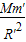 =m′
=m′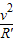
联立解得
R′=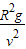
即该空间站轨道半径R′为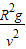 .
.
(2)因为探测器对喷射气体做功的功率恒为P,而单位时间内喷气质量为m,故在t时间内,据动能定理
Pt= mtv2
mtv2
求得喷出气体的速度为
v=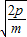
另一方面探测器喷气过程中系统动量守恒,则:
0=mtv-Mu
又
Ek= Mu2
Mu2
联立得探测器获得的动能:
Ek= M(
M(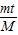 -
- )2=
)2=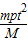
喷气t秒后探测器获得的动能是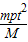 .
.
点评:对于卫星类问题,通常都要用到万有引力等于向心力;应用动能定理要明确研究对象,反冲运动中系统动量一般都守恒!
(2)对t秒内喷出的气体运用动能定理求出喷气速度,再根据动量守恒定律求出探测器的速度,进一步求出探测器的动能.
解答:解:(1)设地球质量为M,在地球表面
g=G
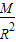
设空间站质量为m′绕地球作匀速圆周运动时
G
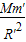 =m′
=m′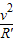
联立解得
R′=
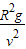
即该空间站轨道半径R′为
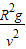 .
.(2)因为探测器对喷射气体做功的功率恒为P,而单位时间内喷气质量为m,故在t时间内,据动能定理
Pt=
 mtv2
mtv2求得喷出气体的速度为
v=
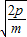
另一方面探测器喷气过程中系统动量守恒,则:
0=mtv-Mu
又
Ek=
 Mu2
Mu2联立得探测器获得的动能:
Ek=
 M(
M(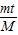 -
- )2=
)2=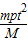
喷气t秒后探测器获得的动能是
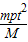 .
.点评:对于卫星类问题,通常都要用到万有引力等于向心力;应用动能定理要明确研究对象,反冲运动中系统动量一般都守恒!

