(1)实验室有一块长方体透明介质,截面如图1所示.AB的长度为l1,AD的长度为l2,且AB和AD边透光,而BC和CD边不透光且射到这两个边的光线均被全部吸收.现让一平行光束以入射角θ1射到AB面,经折射后AD面上有光线射出.甲、乙两同学分别用不同的方法测量该长方体介质的折射率.
甲同学的做法是:保持射到AB面上光线的入射角θ1不变,用一遮光板由A点沿AB缓慢推进,遮光板前端推到P时,AD面上恰好无光线射出,测得AP的长度为l3,则长方体介质的折射率可表示为n= ;
乙同学的做法是:缓慢调节射到AB面上光线的入射角,使AD面也恰好无光线射出.测得此时射到AB面上光线的入射角为θ2,则长方体介质的折射率可表示为n= ; θ1和θ2的关系为:θ1 θ2(填“>”、“<”或“=”).
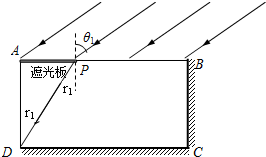
(2)某同学利用红激光做“用双缝干涉测光的波长”的实验时,第一次分划板中心刻度线对齐A条纹中心时,如图2甲所示,游标卡尺的示数如图2丙所示;第二次分划板中心刻度线对齐B条纹中心线时如图2乙所示,游标卡尺的读数如图2丁所示.已知双缝间距为0.5mm,双缝到屏的距离为1m,则图2丙中游标卡尺的读数为 mm,图2丁中游标卡尺的读数为 mm.实验时测量多条干涉条纹宽度的目的是 .所测光波的波长为 m.(保留两位有效数字)
(3)如果实验时将红激光换成蓝激光,屏上相邻两条纹间的距离将 (填变大,变小或不变).
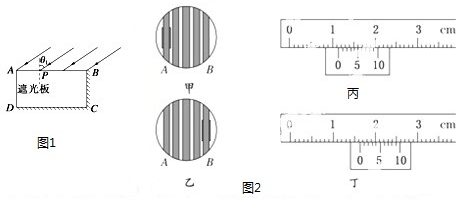
甲同学的做法是:保持射到AB面上光线的入射角θ1不变,用一遮光板由A点沿AB缓慢推进,遮光板前端推到P时,AD面上恰好无光线射出,测得AP的长度为l3,则长方体介质的折射率可表示为n=
乙同学的做法是:缓慢调节射到AB面上光线的入射角,使AD面也恰好无光线射出.测得此时射到AB面上光线的入射角为θ2,则长方体介质的折射率可表示为n=
(2)某同学利用红激光做“用双缝干涉测光的波长”的实验时,第一次分划板中心刻度线对齐A条纹中心时,如图2甲所示,游标卡尺的示数如图2丙所示;第二次分划板中心刻度线对齐B条纹中心线时如图2乙所示,游标卡尺的读数如图2丁所示.已知双缝间距为0.5mm,双缝到屏的距离为1m,则图2丙中游标卡尺的读数为
(3)如果实验时将红激光换成蓝激光,屏上相邻两条纹间的距离将

分析:(1)根据几何知识求出折射角r1,根据折射定律求解折射率.
在AD面上发生全反射,说明在AD面上的入射角等于临界角C.根据临界角公式sinC=
和折射定律结合求解折射率.
由几何关系分析光线在AD面上的入射角与AB面上的折射角的关系,根据在AD面上的入射角越大,越容易发生全反射,分析θ1与θ2的大小.
(2)游标卡尺的读数等于主尺读数加上游标读数,不需估读.根据双缝干涉的条纹间距公式,结合相邻条纹间距的大小求出波长的大小.
(3)根据波长的大小,结合双缝干涉条纹间距公式判断相邻条纹间距的变化.
在AD面上发生全反射,说明在AD面上的入射角等于临界角C.根据临界角公式sinC=
| 1 |
| n |
由几何关系分析光线在AD面上的入射角与AB面上的折射角的关系,根据在AD面上的入射角越大,越容易发生全反射,分析θ1与θ2的大小.
(2)游标卡尺的读数等于主尺读数加上游标读数,不需估读.根据双缝干涉的条纹间距公式,结合相邻条纹间距的大小求出波长的大小.
(3)根据波长的大小,结合双缝干涉条纹间距公式判断相邻条纹间距的变化.
解答:解:(1)设折射角为r1,在△APD中,由几何关系得:
sinr1=
,光在AB面上发生折射,由折射定律可得介质的折射率为:n=
=
.
射到AB面上的光线的入射角为θ2时,在AD面上发生全反射,说明在AD面上的入射角等于临界角.
设在AB面上的折射角为r2,由折射定律得:
=n①
由临界角计算公式得:sinC=
,由几何关系可得:r2+C=90°,
sinr2=sin(90°-C)=cosC=
=
②
由①②联立解得:n=
.
设在AB面上的入射角为r,由几何关系可知在AD面上的入射角为:i=90°-r,在AB面上的折射角越小(即在AB面上的入射角越小),在AD面上的入射角越大,越容易发生全反射,则有θ1>θ2.
(2)图丙中游标卡尺的主尺读数为11mm,游标读数为0.1×5mm=0.5mm,则最终读数为11.5mm.
图丁中游标卡尺的主尺读数为16mm,游标读数为0.1×7mm=0.7mm,则最终读数为16.7mm.
实验时测量多条干涉条纹宽度的目的是减小测条纹间距的误差.相邻条纹间距△x=
mm=1.3mm.
根据△x=
λ得,波长λ=
=
m=6.5×10-7m.
(3)根据△x=
λ知,实验时将红激光换成蓝激光,波长减小,屏上相邻两条纹间的距离将变小.
故答案为:(1)
,
,>;(2)11.5,16.7,可减小测条纹间距的误差,6.5×10-7,(3)变小.
sinr1=
| l3 | ||
|
| sinθ1 |
| sinr1 |
| ||
| l3 |

射到AB面上的光线的入射角为θ2时,在AD面上发生全反射,说明在AD面上的入射角等于临界角.
设在AB面上的折射角为r2,由折射定律得:
| sinθ2 |
| sinr2 |
由临界角计算公式得:sinC=
| 1 |
| n |
sinr2=sin(90°-C)=cosC=
| 1-sin2C |
1-
|
由①②联立解得:n=
| 1+sin2θ2 |
设在AB面上的入射角为r,由几何关系可知在AD面上的入射角为:i=90°-r,在AB面上的折射角越小(即在AB面上的入射角越小),在AD面上的入射角越大,越容易发生全反射,则有θ1>θ2.
(2)图丙中游标卡尺的主尺读数为11mm,游标读数为0.1×5mm=0.5mm,则最终读数为11.5mm.
图丁中游标卡尺的主尺读数为16mm,游标读数为0.1×7mm=0.7mm,则最终读数为16.7mm.
实验时测量多条干涉条纹宽度的目的是减小测条纹间距的误差.相邻条纹间距△x=
| 16.7-11.5 |
| 4 |
根据△x=
| L |
| d |
| △xd |
| L |
| 1.3×10-3×0.5×10-3 |
| 1 |
(3)根据△x=
| L |
| d |
故答案为:(1)
| ||
| l3 |
| 1+sin2θ2 |
点评:在第一问中关键要正确理解全反射的条件,灵活运用几何知识求解折射角.在(2)(3)两问中,关键掌握双缝干涉条纹的间距公式△x=
λ,并能灵活运用.
| L |
| d |

