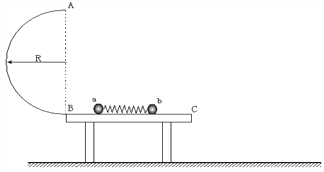
【题目】如图所示，半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上，桌面距水平地面的高度也为R，在桌面上轻质弹簧被a、b两个小球挤压（小球与弹簧不拴接），处于静止状态。同时释放两个小球，小球a、b与弹簧在桌面上分离后，a球从B点滑上半圆环轨道最高点A时速度为，已知小球a质量为m，小球b质量为2m， 重力加速度为g，求：

（1）小球a在圆环轨道最高点对轨道的压力？

（2）释放后小球b离开弹簧时的速度vb的大小？

（3）小球b落地点距桌子右侧的水平距离？

【答案】(1) mg，方向竖直向上 (2) (3)

【解析】（1）设a球通过最高点时受轨道的弹力为N，由牛顿第二定律mg+N＝
得N=mg
由牛顿第三定律，a球对轨道的压力为mg，方向竖直向上．
（2）设小球a与弹簧分离时的速度大小为va，取桌面为零势面，由机械能守恒定律

得
小球a、b从释放到与弹簧分离过程中，总动量守恒mva=2mvb
vb＝
（3）b球从桌面飞出做平抛运动，设水平飞出的距离为x，则R＝gt2

x=vbt
得x＝R

关闭