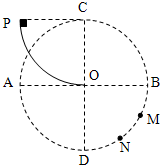
在竖直平面内有一半径为R的圆形区域，AB、CD分别为水平、竖直的两个直径，BM、MN、ND三段弧长相等．有一个长度为四分之一圆的竖直圆弧轨道，半径也是R，圆心在C点，轨道下端在O点与AB相切．
（1）一小滑块从轨道上端P点由静止滑下，若摩擦力的平均值为滑块重力的K倍，重力加速度大小为g，求滑块从O点滑出时的速度大小．
（2）若不计摩擦，滑块仍由静止从轨道上释放，要求滑块离开O点后能落到在圆的MN圆弧上（包括M、N两点），求释放的位置距圆心O的竖直高度．（要求结果用R表示）
分析：（1）小滑块由P到O的过程中，重力和摩擦力做功，根据动能定理求出滑块从O点滑出时的速度大小．
（2）若不计摩擦，滑块仍由静止从轨道上释放，滑块的机械能守恒，即可求出释放的位置距圆心O的竖直高度与滑块到O点的速度关系，由平抛运动的规律得到水平和竖直方向分位移与初速度的关系．如图，三段弧对的圆心角都是30°，为落在MN上，竖直位移应y=Rcos30°≤y≤Rsin30°，联立解得高度．
解答：解：（1）滑块由P到O的过程，由动能定理得：mgR-kmg
πR
2
=
1
2
mv2      
得：v=
(2-kπ)gR
                
（2）根据机械能守恒得：mgh=
1
2
m
v
2
0
                      
从O点平抛后：
  水平方向 x=v0t                        
  竖直方向 y=
1
2
gt2                          
得：v0=x
g
2y
                                  
如图，三段弧对的圆心角都是30°，为落在MN上，
当y=Rcos30°=
3
2
R时，有x≥Rsin30°=
R
2
       
当y=Rsin30°=
R
2
时，有 x≤Rcos30°=
3
2
R      
由以上得：
3
R
24
≤h≤
3
8
h                            
答：
（1）滑块从O点滑出时的速度大小是x
g
2y
．
（2）释放的位置距圆心O的竖直高度是
3
R
24
≤h≤
3
8
h．
点评：本题的关键是确定平抛运动的竖直位移和水平位移的范围，根据数学知识进行分析．
关闭