【题目】一部电动机通过一轻绳从静止开始向上提起质量为m＝4.0 kg的物体，在前2.0 s内绳的拉力恒定，此后电动机保持额定功率P额＝600 W工作，物体被提升至h＝60 m高度时恰好达到最大速度.上述过程的v－t图像如图所示(取g＝10 m/s2，不计空气阻力)，求：

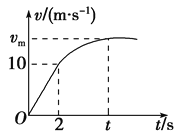
(1)物体的最大速度vm；

(2)物体速度v2＝12 m/s时加速度的大小；

(3)物体从速度v1＝10 m/s时开始，到提升至60 m高度，克服重力所做的功。

【答案】(1) 15 m/s；(2) 2.5 m/s2；(3) 2000 J

【解析】

解析：(1)当拉力F＝mg时，物体达到最大速度vm，由P＝Fv解得vm＝15 m/s

(2)当v2＝12 m/s时电动机以额定功率工作,由P额＝F2v2得：F2＝50 N，由牛顿第二定律得：F2－mg＝ma2，，解得：a2＝2.5 m/s2.

(3)物体匀加速阶段上升高度：h1＝v1t1＝10 m，物体变加速阶段上升高度：h2＝h－h1＝50 m，克服重力所做的功：＝mgh2＝2000 J

关闭