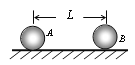
【题目】如图所示,半径相同的两带电小球A、B固定放置在绝缘光滑的水平面上(水平面足够大),A球的质量为2m,带电量为+Q;B球的质量为m,带电量为+q。两球间距为L(L远大于两球半径)。A、B位于彼此产生的电场内,电荷在电场中具有电势能,该能量是系统(两带电体)所共有的。固定A球,释放B球,B球在库仑力的作用下向右加速运动,从释放到运动到足够远(此时两球间的作用力可视为零),根据数学积分可以算出这段过程中库仑力对B球做的功![]() ,k为静电力常数。
,k为静电力常数。
(1)求释放瞬间B球的加速度a的大小,并分析加速度a在运动过程中的变化趋势;
(2)求A球产生的电场在距离L处的电势(规定无穷远处电势为零);
(3)若同时释放两球,求运动到足够远处时B球的速度大小。
参考答案:
【答案】(1)![]() 距离变大,所以a减小。(2)
距离变大,所以a减小。(2)![]() (3)
(3)![]()
【解析】本题考查牛顿第二定律、电势与电势能、动量与能量结合等知识。
(1)选B球为研究对象,释放瞬间对其受力分析,由牛顿第二定律可得: ![]() ,解得:
,解得: ![]()
运动过程中,两球间距离![]() 变大,所以a减小。
变大,所以a减小。
(2)B球从距离A球L处运动到无穷远处过程中有![]() ,又
,又![]() ,联立解得:
,联立解得: ![]()
(3)以AB两球为系统,同时释放两球后,两球动量及能量守恒,则:
![]()
![]()
联立解得: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于热现象和热学规律,下列说法中正确的是_______
A. 悬浮在液体中的微小固定颗粒的运动是无规则的,说明液体分子的运动也是无规则的
B. 物体中分子热运动动能的总和等于物体的内能
C. 在完全失重的情况下,气体对容器壁的压强为零
D. 气体从外界吸收热量,其内能不一定增加
E. 液体表面张力产生的原因是液体表面层分子较稀疏,分子间引力大于斥力
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,物块A和B通过一根轻质不可伸长的细绳连接,跨放在质量不计的光滑定滑轮两侧,质量分别为mA=2 kg、mB=1 kg。初始时A静止于水平地面上,B悬于空中。先将B竖直向上再举高h=1.8 m(未触及滑轮)然后由静止释放。一段时间后细绳绷直,A、B以大小相等的速度一起运动,之后B恰好可以和地面接触。取g=10 m/s2。

(1)B从释放到细绳绷直时的运动时间t;
(2)A的最大速度v的大小;
(3)初始时B离地面的高度H.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学为了验证断电自感现象,自己找来带铁芯的线圈L、小灯泡A、开关S和电池组E , 用导线将它们连接成如图所示的电路.检查电路后,闭合开关S , 小灯泡发光;再断开开关S , 小灯泡仅有不显著的延时熄灭现象.虽然多次重复,仍未见老师演示时出现的小灯泡闪亮现象,他冥思苦想找不出原因.你认为最有可能造成小灯泡未闪亮的原因是( )
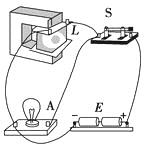
A. 电源的内阻较大
B. 小灯泡电阻偏大
C. 线圈电阻偏大
D. 线圈的自感系数较大
-
科目: 来源: 题型:
查看答案和解析>>【题目】以速度v0竖直向上抛出一物体,空气阻力大小恒定,关于物体受到的冲量,以下说法正确的是( )
A. 物体上升阶段和下降阶段所受重力的冲量方向相反
B. 物体上升阶段和下降阶段所受重力的冲量方向相同
C. 物体在下落阶段受重力的冲量等于上升阶段受重力的冲量
D. 物体从抛出到返回抛出点,物体所受空气阻力的总冲量为零
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一物块仅在三个共点恒力F1、F2、F3的作用下以速度v0水平向右做匀速直线运动,其中F1斜向右上方,F2竖直向下,F3水平向左。某时刻撤去其中的一个力,其他力的大小和方向不变,一段时间后恢复该力,则下列说法不正确的是( )

A. 如果撤去的是F1,则物块先做匀变速曲线运动,恢复该力之后将做直线运动
B. 如果撤去的是F1,恢复F1时物块的速度大小可能为v0
C. 如果撤去的是F3,物块将向右做匀加速直线运动,恢复该力之后做匀速直线运动
D. 如果撤去的是F2,在恢复该力之前的时间内,因物块做曲线运动,故在相等时间间隔内其速度的变化量的方向时刻在改变
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知地球半径为R,高空圆形轨道3距地面高h=2R,椭圆轨道2与贴近地表的轨道1和轨道3分别相切于a、b两点,当卫星分别在这些轨道上运行时,下列说法中正确的是( )

A. 卫星在轨道2上运行至a点和b点时的加速度大小之比为3∶1
B. 卫星分别在轨道1和轨道3上运行时的速度大小之比为3∶1
C. 卫星在轨道2上运行至a、b两点时的机械能之比为1∶3
D. 卫星分别在轨道1、2、3上运行时的周期之比为1∶2
 ∶3
∶3
相关试题

