宇航员到了某星球后做了如下实验:如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ。当圆锥和球一起以周期T匀速转动时,球恰好对锥面无压力.已知星球的半径为R,万有引力常量为G.求: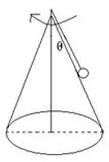
(1)线的拉力;
(2)该星球表面的重力加速度;
(3)该星球的第一宇宙速度;
(4)该星球的密度.
参考答案:
(1)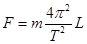 (2)
(2)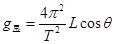
(3)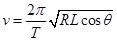 (4)
(4)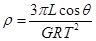
解析试题分析:(1)小球做圆周运动:向心力  ①(1分)
①(1分)
半径 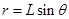 ②(1分)
②(1分)
解得线的拉力 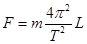 ③(1分)
③(1分)
(2)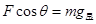 ④(1分)
④(1分)
解得该星球表面的重力加速度 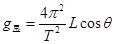 ⑤(2分)
⑤(2分)
(3)星球的第一宇宙速度即为该星球的近“地”卫星的环绕速度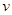 ,设近“地”卫星的质量为
,设近“地”卫星的质量为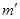 ,根据向心力公式有:
,根据向心力公式有: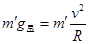 ⑥(1分)
⑥(1分)
联立⑤⑥解得 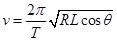 (2分)
(2分)
(4)设星球的质量为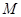 ,则:
,则: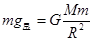 ⑦(1分)
⑦(1分) ⑧(1分)
⑧(1分)
联立⑤⑦⑧⑨解得星球的密度 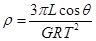 (1分)
(1分)
考点:万有引力定律 第一宇宙速度
-
科目: 来源: 题型:计算题
查看答案和解析>>有一极地卫星绕地球做匀速圆周运动,该卫星的运动周期为T0/4,其中T0为地球的自转周期.已知地球表面的重力加速度为g,地球半径为R..求:
(1)该卫星一昼夜经过赤道上空的次数n为多少?试说明理由。
(2)该卫星离地面的高度H. -
科目: 来源: 题型:计算题
查看答案和解析>>两个行星各有一个卫星绕其表面运行,已知两个卫星的周期之比为1:3,两行星半径之比为3:1,则:
(1)两行星密度之比为多少?
(2)两行星表面处重力加速度之比为多少? -
科目: 来源: 题型:计算题
查看答案和解析>>(9分)在物理学中,常常用等效替代、类比、微小量放大等方法来研究问题。如在牛顿发现万有引力定律一百多年后,卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值,图所示是卡文迪许扭秤实验示意图。卡文迪许的实验常被称为是“称量地球质量”的实验,因为由G的数值及其他已知量,就可计算出地球的质量,卡文迪许也因此被誉为第一个称量地球的人。
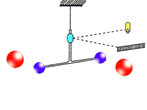
(1)若在某次实验中,卡文迪许测出质量分别为m1、m2相距为r的两个小球之间引力的大小为F,求万有引力常量G;
(2)若已知地球半径为R,地球表面重力加速度为g,万有引力常量为G,忽略地球自转的影响,请推导出地球质量及地球平均密度的表达式。 -
科目: 来源: 题型:计算题
查看答案和解析>>(12分)利用水流和太阳能发电,可以为人类提供清洁能源。水的密度ρ=1×103kg/m3,太阳光垂直照射到地面上时的辐射功率P0 =1×103W/m2,地球半径为R=6.4×106m,地球表面的重力加速度取g=10m/s2。
⑴写出太阳光照射到地球表面的总功率P的字母表达式;
⑵发射一颗卫星到地球同步轨道上(轨道半径约为地球半径的6.6≈ 倍)利用太阳能发电,然后通过微波持续不断地将电力输送到地面,这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小(答案保留两位有效数字);
倍)利用太阳能发电,然后通过微波持续不断地将电力输送到地面,这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小(答案保留两位有效数字);
⑶三峡水电站水库面积约为S=1×109m2,平均流量Q=1.5×104m3/s,水库水面与发电机所在位置的平均高度差为h=100m,发电站将水的势能转化为电能的总效率η1=60%。在地球同步轨道上,太阳光垂直照射时的辐射功率为1.4P0。太阳能电池板将太阳能转化为电能的效率为η2=20%,将电能输送到地面的过程要损失50%。若要使⑵中的太阳能发电站在被太阳照射时地面接收到的电功率相当于三峡电站发电的平均功率,卫星上太阳能电池板的面积应为多大?(保留一位有效数字) -
科目: 来源: 题型:计算题
查看答案和解析>>“嫦娥一号”探月卫星为绕月极地卫星.利用该卫星可对月球进行成像探测.设卫星在绕月极地轨道上做匀速圆周运动时距月球表面的高度为H,绕行周期为TM;月球绕地球公转的周期为TE,轨道半径为R0;地球半径为RE,月球半径为RM.已知光速为c.

(1)如图所示,当绕月极地轨道的平面与月球绕地球公转的轨道平面垂直时(即与地心到月心的连线垂直时),求绕月极地卫星向地球地面发送照片需要的最短时间;
(2)忽略地球引力、太阳引力对绕月卫星的影响,求月球与地球的质量之比. -
科目: 来源: 题型:计算题
查看答案和解析>>(7分)已知地球半径为R,地球表面处的重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v的表达式;
(2)若已知地球自转的周期为T,求地球同步卫星距离地面的高度h。
相关试题

