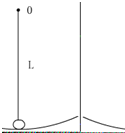
 如图所示,长度为L=1.0m的绳,系一小球在竖直面内绕固定点O做圆周运动,小球的质量为M=1kg,半径不计.若小球在通过最低点时的速度大小为v=4m/s,试求:(取g=10m/s2)
如图所示,长度为L=1.0m的绳,系一小球在竖直面内绕固定点O做圆周运动,小球的质量为M=1kg,半径不计.若小球在通过最低点时的速度大小为v=4m/s,试求:(取g=10m/s2)(1)小球在最低点的向心加速度;
(2)小球在最低点所受绳的拉力.
分析:根据向心加速度的公式求出向心加速度的大小,在最低点靠竖直方向上的合力提供向心力,结合牛顿第二定律求出绳子对小球的拉力.
解答:解:(1)根据向心加速度a=
得:a=
=16m/s2.
(2)在最低点根据牛顿第二定律可得:F-mg=m
解得:F=1×16+1×10=26N.
答:(1)小球在最低点的向心加速度为16m/s2.
(2)小球在最低点所受绳的拉力26N.
| v2 |
| L |
| 16 |
| 1 |
(2)在最低点根据牛顿第二定律可得:F-mg=m
| v2 |
| L |
解得:F=1×16+1×10=26N.
答:(1)小球在最低点的向心加速度为16m/s2.
(2)小球在最低点所受绳的拉力26N.
点评:解决本题的关键搞清向心力的来源,根据牛顿第二定律进行求解.

