搜索
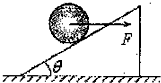
倾角为θ=30°的斜面体放在水平地面上，一个重为G的球在水平力F的作用下，静止在光滑斜面上，则水平力F的大小为
| ||
| 3 |
| ||
| 3 |
| ||
| 6 |
| ||
| 6 |
分析：通过对小球出状态的分析利用共点力平衡条件可求出水平力F的大小，力F方向变化后，对小球受力分析可求得力F与水平方向的角度，因为小球和斜面都处于静止状态，可对整体受力分析求出地面对斜面的摩擦力．
解答：解：对物体受力分析如图：
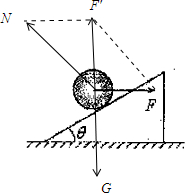
由平衡条件得：N与F的合力F′与重力G大小相等，
由三角函数关系得：tanθ=
=
所以：F=Gtanθ
代入数据得：F=
G
转过角度后，由F大小不变，小球静止，支持力与F的合力不变，故此时转动后F转方向如图：
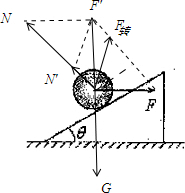
即：F转过的角度是2θ．
对整体受力分析并正交分解如图：
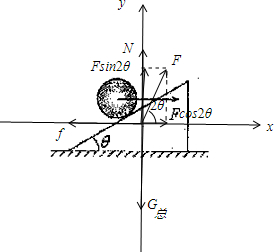
水平方向：f=Fcos2θ=
×
=
G
故答案为：
G；
G．
由平衡条件得：N与F的合力F′与重力G大小相等，
由三角函数关系得：tanθ=
| F |
| F′ |
| F |
| G |
所以：F=Gtanθ
代入数据得：F=
| ||
| 3 |
转过角度后，由F大小不变，小球静止，支持力与F的合力不变，故此时转动后F转方向如图：
即：F转过的角度是2θ．
对整体受力分析并正交分解如图：
水平方向：f=Fcos2θ=
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
故答案为：
| ||
| 3 |
| ||
| 6 |
点评：此题关键还是平衡条件的应用，难点在于选择合适的研究对象和找出力F转动后的角度，有难度，需要仔细推敲体会．
