【题目】如图所示,倾角为θ、动摩擦因数为![]() 的足够长粗糙斜面
的足够长粗糙斜面![]() 与内壁光滑的竖直圆弧形轨道
与内壁光滑的竖直圆弧形轨道![]() 相切于B点,圆弧轨道的半径为R,
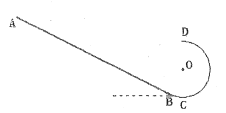
相切于B点,圆弧轨道的半径为R,![]() 连线为圆弧轨道的竖直直径。甲和乙是两个质量均为m的相同小球(可视为质点),乙静止在C点处,将甲从斜面上某处无初速度释放,甲、乙在C点发生正碰后粘在一起,此后恰能通过圆轨道最高点D。求:
连线为圆弧轨道的竖直直径。甲和乙是两个质量均为m的相同小球(可视为质点),乙静止在C点处,将甲从斜面上某处无初速度释放,甲、乙在C点发生正碰后粘在一起,此后恰能通过圆轨道最高点D。求:
(1)小球甲与乙碰撞前瞬间的速度大小;
(2)小球甲在斜面上运动的位移大小。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)甲球和乙球在C处碰撞,动量守恒,设甲球在碰撞前的速度为![]() ,则有
,则有
![]()
碰后,甲乙两球刚好能运动到D点,在D点,有:![]()
从C到D,由机械能守恒定律得:![]()
联立以上式子解得:![]()
(2)对甲球,从A到C,由动能定理得:![]()
R(1﹣cosθ)+sABsinθ=h
解得:![]()

