搜索
(15分) 如图所示为半径R=0.50m的四分之一圆弧轨道，底端距水平地面的高度h=0.45m。一质量m=1.0kg的小滑块从圆弧轨道顶端A由静止释放，到达轨道底端B点的速度v = 2.0m/s。忽略空气的阻力。取g=10m/s2。
求：
（1）小滑块在圆弧轨道底端B点受到的支持力大小FN；
（2）小滑块由A到B的过程中，克服摩擦力所做的功W；
（3）小滑块落地点与B点的水平距离x。
（1）
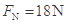（2）3J（3）0.6m
解析试题分析：（1）根据牛顿第二定律， 
(3分)
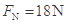解得： (2分)
（2）根据动能定理，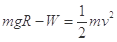 
(3分)
解得：
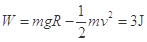(2分)
（3）水平方向：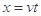 
(2分)
竖直方向：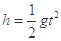 
(2分)
解得：
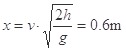(1分)
考点：考查了牛顿第二定律以及动能定理的应用
点评：物体的运动分为两个过程，分析清楚两个过程中各个力做功的情况后，可以用动能定理列式求解，同时要注意能用机械能守恒定律求解的问题都能用动能定理求解！
