练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情

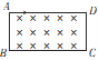
    【题目】如图所示，在矩形区域(含边界)存在垂直纸面向里的匀强磁场，磁感应强度大小B0=2.0×10-2T，A、B、C、D为矩形的四个顶点，BC边长l1=4m，AB边长l2=2m。大量质量m=3.2×10-26kg、带电荷量q=-1.6×10-18C的粒子，从A点沿AD方向以不同的速率射入匀强磁场中，粒子恰好均从BC边射出，不计粒子重力及粒子间的作用力。求：

    （1）粒子的速率的取值范围；

    （2）粒子在磁场中运动的最长时间。

    【答案】（1）；（2）

    【解析】

    (1)粒子恰好均从BC边射出，可知粒子以最小速率v1运动时恰好打在B点，由几何关系可知其半径

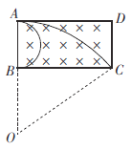
    可知粒子以最大速率v2运动时恰好打在C点，设其半径为R2，由几何关系

    解得

    m

    粒子在匀强磁场中运动，由洛伦兹力提供向心力，有

    可得

    解得

    则粒子的速率的取值范围为

    (2)从B点射出的粒子在磁场中运动的时间最长，其运动时间

    而

    解得

    s

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    【题目】某同学利用下述装置对轻质弹簧的弹性势能进行探究，一轻质弹簧放置在光滑水平桌面上，弹簧左端固定，右端与一小球接触而不固连:弹簧处于原长时，小球恰好在桌面边缘，如图（a）所示。向左推小球，使弹簧压缩一段距离后由静止释放。小球离开桌面后落到水平地面。通过测量和计算，可求得弹簧被压缩后的弹性势能。

    回答下列问题：

    （1）本实验中可认为，弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等。已知重力加速度大小为g，为求得Ek，至少需要测量下列物理量中的 （填正确答案标号）。

    A．小球的质量m

    B．小球抛出点到落地点的水平距离s

    C．桌面到地面的高度h

    D．弹簧的压缩量△x

    E.弹簧原长l0

    （2）用所选取的测量量和已知量表示Ek，得Ek= 。

    （3）图（b）中的直线是实验测量得到的s—△x图线。从理论上可推出，如果h不变。m增加，s—△x图线的斜率会 （填“增大”、“减小”或“不变”）；如果m不变，h增加，s—△x图线的斜率会 （填“增大”、“减小”或“不变”）。由图（b）中给出的直线关系和Ek的表达式可知，Ep与△x的 次方成正比。

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】如图所示，A、B、C三个一样的滑块从粗糙斜面上的同一高度同时开始运动。A由静止释放；B的初速度方向沿斜面向下，大小为v0；C的初速度方向沿水平方向，大小为v0。斜面足够大，A、B、C运动过程中不会相碰，下列说法正确的是（　　）

    A.A和C将同时滑到斜面底端

    B.滑到斜面底端时，B的动能最大

    C.滑到斜面底端时，C的重力势能减少最多

    D.滑到斜面底端时，C的机械能减少最多

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】如图甲所示的装置叫做阿特伍德机，是英国数学家和物理学家阿特伍德（G·Atwood746-1807）创制的一和著名力学实验装置，用来研究匀变速直线运动的规律。某同学对该装置加以改进后用来验证机械能守恒定律和动量守恒定律，如图乙所示。（已知当地的重力加速度为g）

    (1)该同学用游标卡尺测量遮光片的宽度如图丙所示，则d=___________mm；然后将质量均为m（A的含挡光片和挂钩、B的含挂钩）的重物用绳连接后，跨放在定滑轮上，A置于桌面上处于静止状态，测量出挡光片中心到固定光电门中心的竖直距离h。

    (2)为了验证动量守恒定律，该同学让A在桌面上处丁静止状态，将乃从静止位置竖直提升s后由自由下落，光电门记录下挡光片挡光的时间为Δt（B未接触桌面），则验证绳绷紧过程中系统治绳方向动量守恒定律的表达式为__________；如果该同学忘记将B下方的C取下（C的质量也为m），光电门记录挡光片挡光的时间为△t′。完成测量后，骑证动量守恒定律的表达式为__________。（用题中所给物理量符号表示）

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】已知电流大小为I的长直导线在离长直导线r距离处产生磁场的磁感应强度大小B=k(k为比例系数，r为该点到导线的距离，I为导线的电流大小)。如图所示，在一半径为R的圆形区域内的圆心O处放置一电流大小为I的长直导线a，导线电流方向垂直纸面向外，纸面内圆心O点右侧2R处有另一长直导线b，电流大小也为I、方向如图所示，N为圆心O到导线b距离的中点，其中导线a在N点产生磁场的磁感应强度大小为B0。下列说法正确的是（ ）

    A.导线b产生的磁场穿过该圆形区域的磁通量为零

    B.导线b在N点产生的磁场的磁感应强度大小为B0、方向垂直纸面向外

    C.导线b在圆心O点产生的磁场的磁感应强度大小为2B0、方向垂直纸面向外

    D.导线a和导线b在N点产生磁场的合磁感应强度大小为B0

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】如图所示，小球放在光滑的墙与装有铰链的光滑薄板之间，薄板在F作用下逆时针缓慢转动，在墙与薄板之间的夹角θ缓慢地从90°逐渐减小的过程中（ ）

    A.小球对薄板的压力可能小于小球的重力

    B.小球对薄板的正压力一直增大

    C.小球对墙的压力先减小，后增大

    D.小球对墙的正压力不可能大于小球的重力

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】光电门是一种较为精确的测时装置，某同学使用光电门和其他仪器设计了如图所示的装置来验证机械能守恒定律。A为装有挡光片的钩码，总质量用m表示，已知挡光片的挡光宽度为b，轻绳一端与A相连，另一端跨过光滑轻质定滑轮与的重物B相连，B的质量用M表示（并保证：M<m），他的做法是：先用力拉住B，保持A、B静止，用h表示A的挡光片上端到光电门的距离；然后由静止释放B，A下落过程中经过光电门，光电门可测出挡光片的挡光时间t，算出挡光片经过光电门的平均速度，将其视为A下落h（hb）时的速度，重力加速度为g。

    (1)为了完成上述实验，除了图示给出的实验器材以外，还需要的实验器材有：________；

    (2)在A从静止开始下落h的过程中，验证以A、B、地球所组成的系统机械能守恒的表达式为_______（用题目所给物理量的符号表示）；

    (3)由于光电门所测的平均速度与物体A下落h时的瞬时速度间存在一个差值△v，因而系统减少的重力势能________系统增加的动能（选填“大于”或“小于”）；

    (4)为减小上述△v对结果的影响，该同学想到了以下一些做法，其中可行的是_______。

    A.适当减小挡光片的挡光宽度b

    B.增大挡光片的挡光宽度b

    C.减小挡光片上端到光电门的距离h

    D.保持A下落的初始位置不变，测出多组t，算出多个平均速度然后取平均值

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】如图，A代表一个静止在地球赤道上的物体、B代表一颗绕地心做匀速圆周运动的近地卫星，C代表一颗地球同步轨道卫星。比较A、B、C绕地心的运动，说法正确的是（　　）

    A.运行速度最大的一定是BB.运行周期最长的一定是B

    C.向心加速度最小的一定是CD.受到万有引力最小的一定是A

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    【题目】如图所示，质量为M=lkg、半径为R=lm的圆弧体以放在水平面上，圆弧面的最低端B点刚好与水平面相切，B点左侧水平面粗糙右侧光滑，质量为m=0. 5kg的物块b放在水平面上的A点。现使物块b以大小为v0=4m/s的初速度向右滑去，并刚好能滑到圆弧面上的最高点C，A、B间的距离为L=lm，物块b与B点左侧水平面间的动摩擦因数为，重力加速度g取10 m/s2，。

    (1)求圆弧面所对的圆心角；

    (2)若A、B间水平面光滑，将圆弧体固定，物块仍以v0的初速度向右滑去，则物块从C点抛出后，经多长时间落地？（结果可用根式表示）

    查看答案和解析>>

    同步练习册答案