Question

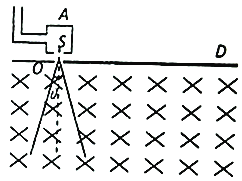
【题目】利用电场和磁场，可以将比荷不同的离子分开，这种方法在化学分析和原子核技术等领域有重要的应用，如图所示碳14和碳12经电离后的原子核带电量均为q，从容器A下方小孔S不断飘入电势差为U的加速电场，经过S正下方小孔O后，沿SO方向垂直进入磁感应强度为B，方向垂直纸面向里的匀强磁场中，最后打在照相底片D上并被吸收，D与O在同一水平面上，其中碳12的粒子在OD上的落点距O点为d，已知粒子经过小孔S时的速度可视为零，不考虑粒子重力，

（1）求粒子碳12的比荷；

（2）由于粒子相互作用，所有粒子分布在与Os竖直方向成一定夹角θ的纸面内，要使两种粒子运动到OD直线上时能区分在不同区域，求θ角的最大值；（可以用三角函数表示）

（3）实际上加速电压的大小会在范围内微小变化，当时，碳14与碳12经电场加速后进入磁场中发生分离，为使这两种粒子在照相底片上落地区域不发生重叠，应满足什么条件？