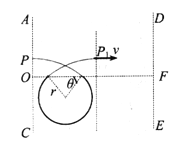
【题目】如图所示，在无限长的竖直边界AC和DE间，上、下部分分别充满方向垂直于ADEC平面向外的匀强磁场，上部分区域的磁感应强度大小为B0，OF为上、下磁场的水平分界线。质量为m、带电荷量为+q的粒子从AC边界上与O点相距为a的P点垂直于A C边界射入上方区域，经OF上的Q点第一次进入下方区域，Q与O点的距离为3a。不考虑粒子重力

(1)求粒子射入时的速度大小；

(2)要使粒子不从AC边界飞出，求下方区域的磁感应强度应满足的条件；

(3)若下方区域的磁感应强度B=3B0，粒子最终垂直DE边界飞出，求边界DE与AC 间距离的可能值。

【答案】（1）；（2）；（3）

【解析】试题分析：（1）设粒子在OF上方做圆周运动半径为R，由几何关系可知；

，

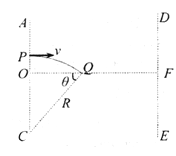
由牛顿第二定律可知： ，解得： ；

（2）当粒子恰好不从AC边界飞出时，设粒子在OF下方做圆周运动的半径为，

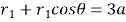
由几何关系得： ， ，所以，根据

解得： ，当时，粒子不会从AC边界飞出。

（3）当时，粒子在OF下方的运动半径为： ，设粒子的速度方向再次与射入磁场时的速度方向一致时的位置为，则P与的连线一定与OF平行，根据几何关系知： ；所以若粒子最终垂直DE边界飞出，边界DE与AC间的距离为： ；

关闭