【题目】如图所示，真空中的、为两个等大的均匀带电圆环，其圆心分别为、，带电量分别为、，将它们平行放置，、连线垂直于圆环平面，为的中点，现有质量为、带电量为的微粒（重力不计）从左方沿、连线方向射入，到点时速度，到点时速度，取无穷远处为电势零点，点电荷的电势公式为，式中为静电力常量，为点电荷的电量，为到点电荷的距离，则（　　）

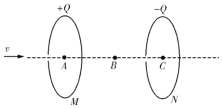
A.微粒从至做加速运动，且

B.微粒越过点后先做加速运动，后做减速运动

C.微粒将以为中心做往返运动

D.微粒在整个运动过程中的最终速度为

【答案】ABD

【解析】

A．由题意可知由至电场向右，微粒所受电场力向右，故从到微粒做加速运动，由对称性可知，粒子由至与由至电场力做的功相同，故动能的变化量相同，故有

代入数据可得，故A正确；

B．根据电场分布的特点可知微粒越过点后开始阶段电场力向右，微粒做加速运动；后面电场力向左，微粒做减速运动，故B正确；

CD．由对称性可知，整个图形的中垂线为等势线，取无穷远处为零势点时此线即为零势线，粒子由点运动到无穷远处，电势未发生变化，电场力做功为零，故粒子最终的速率与点的速率相等，即为最终速度为，微粒不会返回B点，故C错误，D正确。

故选ABD。

关闭