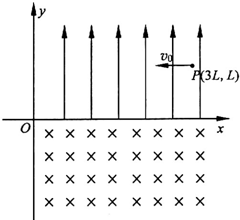
 如图所示,在xOy坐标平面的第一象限内存在一沿y轴正方向的匀强电场,在第四象限内存在一垂直于xOy平面向里的匀强磁场.现有一电子(质量为m、电荷量大小为e)以初速度υ0从电场中坐标为(3L,L)的P点沿垂直于场强方向射入,然后从x轴上的A点(图中未画出)射入磁场.已知电场强度大小为E=
如图所示,在xOy坐标平面的第一象限内存在一沿y轴正方向的匀强电场,在第四象限内存在一垂直于xOy平面向里的匀强磁场.现有一电子(质量为m、电荷量大小为e)以初速度υ0从电场中坐标为(3L,L)的P点沿垂直于场强方向射入,然后从x轴上的A点(图中未画出)射入磁场.已知电场强度大小为E=m
| ||
| 2eL |
| 2mv0 |
| eL |
(1)电子在A点的速度大小及速度方向与x轴负方向的夹角;
(2)电子从磁场中出射点的位置坐标;
(3)电子在磁场中运动所用的时间.
分析:电子在电场中做类平抛运动,根据平抛运动规律可求解电子在A点的速度;
根据平抛运动规律求得电子眼x方向的位移,从而可知电子入射点的横坐标,电子在磁场中由于洛伦兹力作用做圆周运动,结合几何关系可求得出射点位置坐标;
根据电子在磁场中的偏转可求解运动时间.
根据平抛运动规律求得电子眼x方向的位移,从而可知电子入射点的横坐标,电子在磁场中由于洛伦兹力作用做圆周运动,结合几何关系可求得出射点位置坐标;
根据电子在磁场中的偏转可求解运动时间.
解答:解:(1)电子在电场中做类平抛运动,从P点到A点过程:eE=ma
L=
a
vy=at1
解得:vy=v0
故电子在A点的速度vA=
=
v0
设vA与x轴负方向夹角为θ
则tanθ=
=1
即θ=45°;
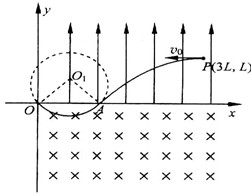
(2)电子在电场中做类平抛运动,沿x方向的位移:
x=v0t1=2L
A点到O点的距离:xA=3L-x=L
电子在磁场中做圆周运动:evAB=
故R=
解得:R=
L
则圆周在x轴上的弦长:△x=2Rcos45°=L
即电子从云强磁场中出射点的位置坐标为O(0,0)
(3)电子在磁场中运动的周期:T=
=
故电子在磁场中运动所用的时间:t=
T=
答:(1)电子在A点的速度大小为
v0,速度方向与x轴负方向的夹角为45°;
(2)电子从磁场中出射点的位置坐标为O(0,0);
(3)电子在磁场中运动所用的时间为
.
L=
| 1 |
| 2 |
| t | 2 1 |
vy=at1
解得:vy=v0
故电子在A点的速度vA=
|
| 2 |
设vA与x轴负方向夹角为θ
则tanθ=
| vy |
| v0 |
即θ=45°;
(2)电子在电场中做类平抛运动,沿x方向的位移:
x=v0t1=2L
A点到O点的距离:xA=3L-x=L
电子在磁场中做圆周运动:evAB=
m
| ||
| R |
故R=
| mvA |
| eB |
解得:R=
| ||
| 2 |
则圆周在x轴上的弦长:△x=2Rcos45°=L
即电子从云强磁场中出射点的位置坐标为O(0,0)
(3)电子在磁场中运动的周期:T=
| 2πm |
| eB |
| πL |
| v0 |
故电子在磁场中运动所用的时间:t=
| 1 |
| 4 |
| πL |
| 4v0 |

答:(1)电子在A点的速度大小为
| 2 |
(2)电子从磁场中出射点的位置坐标为O(0,0);
(3)电子在磁场中运动所用的时间为
| πL |
| 4v0 |
点评:电子在电场中做类平抛运动的研究方法是运动的分解,而磁场中圆周运动的研究常根据轨迹图结合几何关系求解,都是常用的思路,难度不大.

