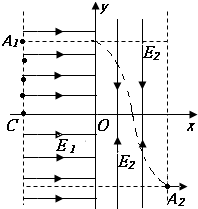
 如图所示的直角坐标系中,在直线x=-d到y轴区域内存在着水平向右的匀强电场E1;在直线x=d到y轴区域存在着两个大小均为E2、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A1(-d,d)到C(-d,0)区域内,连续分布着电量为+q、质量为m的粒子,且均处于静止状态.若处于A1点的粒子,在电场力作用下,能恰好从右边电场的边界A2(d,-d)处沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用:
如图所示的直角坐标系中,在直线x=-d到y轴区域内存在着水平向右的匀强电场E1;在直线x=d到y轴区域存在着两个大小均为E2、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A1(-d,d)到C(-d,0)区域内,连续分布着电量为+q、质量为m的粒子,且均处于静止状态.若处于A1点的粒子,在电场力作用下,能恰好从右边电场的边界A2(d,-d)处沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用:(1)匀强电场的电场强度E1与E2之比;
(2)在A1C间还有哪些位置的粒子,通过电场后也能沿x轴正方向运动.
分析:带电粒子先类平抛后类斜抛,根据运动的合成与分解进行求解
解答:解:(1)粒子在y轴左侧的电场中做匀加速直线运动,电场力做功等于动能的增加,得:qE1d=
mv2
粒子能恰好从右边电场的边界A2(d,-d)处沿x轴正方向射出电场,则粒子在右侧电场中的运动具有上下的对称性,所以,粒子在x轴上方的电场中有:
=vt,a=
,d=
at2
联立以上公式,解得:
=
(2)设距离x轴距离为y的粒子通过电场后也能沿x轴正方向运动,则则第一次达到x轴离开原点为:x0=
(n=1,2,3…)
时间:t0=
所以:y=
a
=
=
(n=1,2,3…)
答:(1)匀强电场的电场强度E1与E2之比
=
;
(2)在A1C间满足条件:y=
(n=1,2,3…)的粒子,通过电场后也能沿x轴正方向运动.
| 1 |
| 2 |
粒子能恰好从右边电场的边界A2(d,-d)处沿x轴正方向射出电场,则粒子在右侧电场中的运动具有上下的对称性,所以,粒子在x轴上方的电场中有:
| d |
| 2 |
| qE2 |
| m |
| 1 |
| 2 |
联立以上公式,解得:
| E1 |
| E2 |
| 1 |
| 16 |
(2)设距离x轴距离为y的粒子通过电场后也能沿x轴正方向运动,则则第一次达到x轴离开原点为:x0=
| d |
| 2n |
时间:t0=
| x0 |
| v |
所以:y=
| 1 |
| 2 |
| t | 2 0 |
| E2a |
| 16n2E1 |
| d |
| n2 |
答:(1)匀强电场的电场强度E1与E2之比
| E1 |
| E2 |
| 1 |
| 16 |
(2)在A1C间满足条件:y=
| d |
| n2 |
点评:本题考查了带电粒子在电场中的运动,难点是确定通过电场后也能沿x轴正方向运动的粒子的条件.

