搜索
附加题．如图甲所示，一竖直的轨道由粗糙斜面 AD 和光滑圆轨道DCE组成，AD与DCE相切于D点，C为圆轨道的最低点，弧DC所对的圆心角θ=37°，半径R=1m．将质量m=0.5kg的物块置于轨道 ADC 上离地面高为 H处由静止释放，物体与斜面 AD 间的动摩擦因数μ=0.6，用力传感器测出其经过C点时对轨道的压力N，改变 H 的大小，可测出相应的 N 大小，试直接给出小物块到C点时对轨道的压力N随 H的关系式，并作出N随H的变化关系图．（不要求解题过程，重力加速度g取 10m/s2）．
分析：分两种情况根据动能定理及向心力公式列式求解N与H的关系式，进而画出图象．
解答：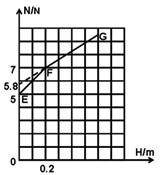
解：（1）如果物块只在圆规道上运动，
mgH=
mv2
由向心力公式得：
N-mg=m
解得：N=
H+mg=(10H+5)N
（2）如果物块由斜面上滑下，则
mgH-μmgcosθ(H-0.2)•
=
mv2
由向心力公式得：
N-mg=m
解得：N=（2H+6.6）N
所以图象如图所示：
解：（1）如果物块只在圆规道上运动，mgH=
| 1 |
| 2 |
由向心力公式得：
N-mg=m
| v2 |
| R |
解得：N=
| 2mg |
| R |
（2）如果物块由斜面上滑下，则
mgH-μmgcosθ(H-0.2)•
| 1 |
| sinθ |
| 1 |
| 2 |
由向心力公式得：
N-mg=m
| v2 |
| R |
解得：N=（2H+6.6）N
所以图象如图所示：
点评：本题主要考查了动能定理及向心力公式的直接应用，要求同学们能根据表达式画出图象，难度适中．
