【题目】如图1，在四边形ABCD中，AD∥BC，BC=2AD，E，F分别为AD，BC的中点，AE=EF，．将四边形ABFE沿EF折起，使平面ABFE⊥平面EFCD（如图2），G是BF的中点．

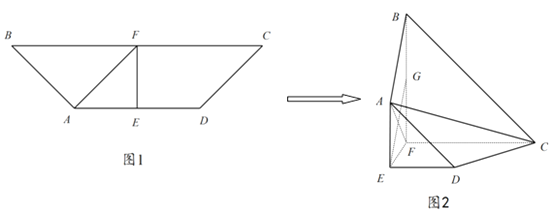
（1）证明：AC⊥EG；

（2）在线段BC上是否存在一点H，使得DH∥平面ABFE？若存在，求的值；若不存在，说明理由；

（3）求二面角D-AC-F的大小．

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）推导出，，，从而平面，进而，四边形为正方形，，由此能证明平面，从而；（2）由，，两两垂直，建立空间直角坐标系，由此利用向量法能求出在线段上存在一点，使得平面，并能求出的值；（3）求出平面的法向理和平面的法向量，利用向量法能求出二面角的大小．

证明：（1）在图1中，，

可得△AEF为等腰直角三角形，AE⊥EF．

因为AD∥BC，所以EF⊥BF，EF⊥FC．

因为平面ABFE⊥平面EFCD，且两平面交于EF，CF平面CDEF，

所以CF⊥平面ABFE．

又EG平面ABFE，故CF⊥EG；

由G为中点，可知四边形AEFG为正方形，所以AF⊥EG；

又AF∩FC=F，所以EG⊥平面AFC．又AC平面AFC，所以AC⊥EG

（2）由（1）知：FE，FC，FB两两垂直，如图建立空间直角坐标系F-xyz，

设FE=1，则F（0，0，0），C（0，2，0），B（0，0，2），D（1，1，0）．

设H是线段BC上一点，．

因此点．

由（1）知为平面ABFE的法向量，=（0，2，0），

因为平面ABFE，所以平面，当且仅当，

即，解得．

．

（3）设A（1，0，1），E（1，0，0），G（0，0，1）．

由（1）可得，是平面的法向量，．，

设平面ACD的法向量为n=（x，y，z），

由即

令x=1，则y=1，z=1．于是n=（1，1，1）．

所以．

所以二面角D-AC-F的大小为90°

关闭