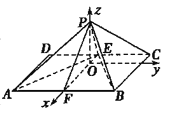
【题目】如图,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
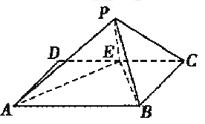
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)先由线面垂直的判定定理得到![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;
;
(2)先取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,证明平面
,证明平面![]() 平面
平面![]() ,在平面
,在平面![]() 内作
内作![]() 于
于![]() 点,则
点,则![]() 平面
平面![]() . 以
. 以![]() 点为原点,
点为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,如图建立空间直角坐标系.分别求出两平面的法向量,求向量夹角余弦值,即可求出结果.
轴,如图建立空间直角坐标系.分别求出两平面的法向量,求向量夹角余弦值,即可求出结果.
(1)因为四边形![]() 是正方形,所以折起后
是正方形,所以折起后![]() ,且
,且![]() ,
,
因为![]() ,所以
,所以![]() 是正三角形,所以
是正三角形,所以![]() .
.
又因为正方形![]() 中,
中,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,则
,则![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
在平面![]() 内作
内作![]() 于
于![]() 点,则
点,则![]() 平面
平面![]() .
.
以![]() 点为原点,
点为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由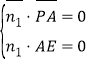 ,得
,得
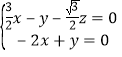 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
∴![]() .
.
因为平面![]() 的法向量为
的法向量为![]() ,
,
则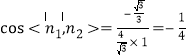 ,
,
又二面角![]() 为锐二面角,∴二面角
为锐二面角,∴二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
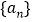 满足,
满足,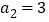 ,
,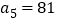 .
.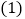 求数列
求数列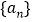 的通项公式;
的通项公式;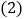 设
设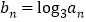 ,求
,求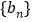 的前n项和为
的前n项和为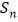 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比在B地晚
 秒. A地测得该仪器弹至最高点H时的仰角为30°.
秒. A地测得该仪器弹至最高点H时的仰角为30°.(1)求A、C两地的距离;
(2)求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆
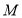 :
: 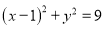 ,点
,点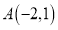 .
.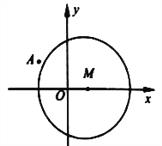
(1)求经过点
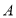 且与圆
且与圆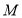 相切的直线
相切的直线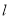 的方程;
的方程;(2)过点
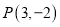 的直线与圆
的直线与圆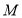 相交于
相交于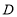 、
、 两点,
两点, 为线段
为线段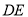 的中点,求线段
的中点,求线段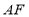 长度的取值范围.
长度的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】米勒问题,是指德国数学家米勒1471年向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆呈现最长(即可见角最大?)米勒问题的数学模型如下:如图,设
 是锐角
是锐角 的一边
的一边 上的两定点,点
上的两定点,点 是边
是边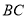 边上的一动点,则当且仅当
边上的一动点,则当且仅当 的外接圆与边
的外接圆与边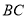 相切时,
相切时, 最大.若
最大.若 ,点
,点 在
在 轴上,则当
轴上,则当 最大时,点
最大时,点 的坐标为( )
的坐标为( )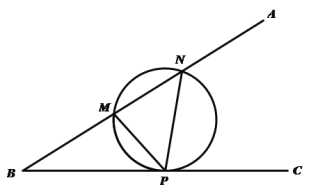
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高二年级共有800名学生参加2019年全国高中数学联赛江苏赛区初赛,为了解学生成绩,现随机抽取40名学生的成绩(单位:分),并列成如下表所示的频数分布表:
分组




频数





⑴试估计该年级成绩不低于90分的学生人数;
⑵成绩在
 的5名学生中有3名男生,2名女生,现从中选出2名学生参加访谈,求恰好选中一名男生一名女生的概率.
的5名学生中有3名男生,2名女生,现从中选出2名学生参加访谈,求恰好选中一名男生一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,已知圆
中,已知圆 :
: .
.
⑴若圆
 的半径为2,圆
的半径为2,圆 与
与 轴相切且与圆
轴相切且与圆 外切,求圆
外切,求圆 的标准方程;
的标准方程;⑵若过原点
 的直线
的直线 与圆
与圆 相交于
相交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
相关试题

