【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
参考答案:
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ;(ⅱ)99万元
;(ⅱ)99万元
【解析】试题分析:(1)根据平均值为![]() ;(2)(ⅰ)先求得
;(2)(ⅰ)先求得![]() ;
; ![]() ,由
,由![]() ,得
,得![]() .解得
.解得![]() ;(ⅱ)易得这款保险产品的保费收入为
;(ⅱ)易得这款保险产品的保费收入为![]()
![]() 当
当![]() ,即每份保单的保费为60元时,保费收入最大为360万元
,即每份保单的保费为60元时,保费收入最大为360万元![]() 预计这款保险产品的最大利润为
预计这款保险产品的最大利润为![]() 万元.
万元.
试题解析:(1)收益率的平均值为![]()
![]() .
.
(2)(ⅰ)![]() ;
;
![]()
由![]() ,得
,得![]() .解得
.解得![]() .
.
(ⅱ)设每份保单的保费为![]() 元,则销量为
元,则销量为![]() .
.
则这款保险产品的保费收入为![]() 万元.
万元.
于是, ![]() .
.
所以,当![]() ,即每份保单的保费为60元时,保费收入最大为360万元.
,即每份保单的保费为60元时,保费收入最大为360万元.
预计这款保险产品的最大利润为![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
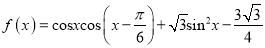 .
.(1)求
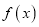 的最小正周期
的最小正周期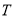 ;
;(2)设
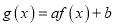 ,若
,若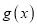 在
在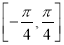 上的值域为
上的值域为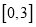 ,求实数
,求实数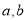 的值;
的值;(3)若
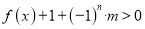 对任意的
对任意的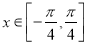 和
和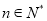 恒成立,求实数
恒成立,求实数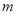 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
-
科目: 来源: 题型:
查看答案和解析>>【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表:
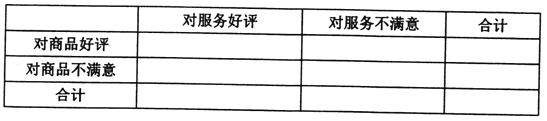
(2)通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;

-
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:
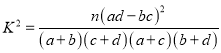 ,
, 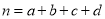 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+x2-xlna,a>1.
(1)求证:函数f(x)在(0,+∞)上单调递增;
(2)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公元
 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
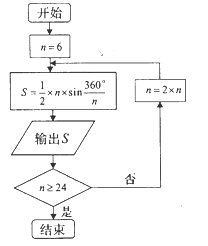
年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值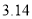 ,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中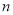 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )(参考数据:
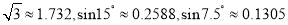 )
)
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
相关试题

