【题目】在平面直角坐标系中,O为原点,两个点列![]() 和
和![]() 满足:①
满足:①![]() ;②
;②![]()
(1)求点![]() 和
和![]() 的坐标;
的坐标;
(2)求向量![]() 的坐标;
的坐标;
(3)对于正整数k,用![]() 表示无穷数列
表示无穷数列![]() 中从第k+1项开始的各项之和,用
中从第k+1项开始的各项之和,用![]() 表示无穷数列
表示无穷数列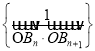 中从第k项开始的各项之和,即
中从第k项开始的各项之和,即![]() ,
,![]() 若存在正整数k和p,使得
若存在正整数k和p,使得![]() ,求k,p的值.
,求k,p的值.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)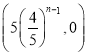 ,
,![]() ;(3)见解析
;(3)见解析
【解析】
(1)求出![]() ,从而
,从而![]() ,
,![]() ,由此能求出点A3和B3的坐标.
,由此能求出点A3和B3的坐标.
(2)由AnAn+1=(![]() )n﹣1A1A2=(﹣(
)n﹣1A1A2=(﹣(![]() )n﹣1,0),得到
)n﹣1,0),得到![]() ,由此能求出向量
,由此能求出向量![]() ,
,![]() 的坐标.
的坐标.
(3)由|![]() |=5(
|=5(![]() )n﹣1,得
)n﹣1,得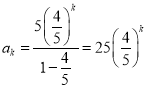 ,
,![]() ,从而25(
,从而25(![]() )k=2kp,由此能求出结果.
)k=2kp,由此能求出结果.
(1)![]() ,故
,故![]() ,即
,即![]() ;
;![]() ,故
,故![]() ,即
,即![]()
(2)由已知,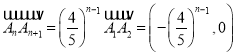 ,
,
故![]() =
=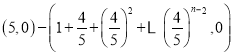 =
=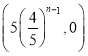
而![]() ;
;
(3)![]() ,
,![]() ,
,
故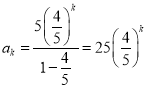 ,
,![]() ,
,
由已知,![]() ,所以,左边为正整数,故k=1或2;
,所以,左边为正整数,故k=1或2;
当k=1时,2p=20,得p=10;
当k=2时,4p=16,得p=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以坐标原点为极点,
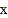 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线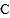 的极坐标方程为
的极坐标方程为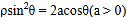 ,过点
,过点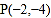 的直线
的直线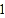 的参数方程为
的参数方程为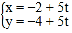 (
( 为参数),直线
为参数),直线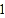 与曲线
与曲线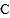 相交于
相交于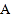 ,
,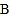 两点.
两点.(1)写出曲线
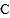 的直角坐标方程和直线
的直角坐标方程和直线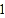 的普通方程;
的普通方程;(2)若
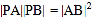 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴
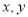 的交点为
的交点为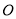 ,与
,与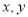 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是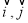 ,且
,且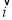 与
与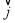 的夹角为
的夹角为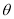 ,其中
,其中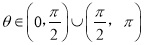 。由平面向量基本定理,对于平面内的向量
。由平面向量基本定理,对于平面内的向量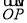 ,存在唯一有序实数对
,存在唯一有序实数对 ,使得
,使得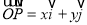 ,把
,把 叫做点
叫做点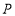 在斜坐标系
在斜坐标系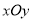 中的坐标,也叫做向量
中的坐标,也叫做向量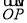 在斜坐标系
在斜坐标系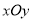 中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如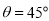 时,方程
时,方程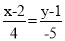 表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。(1)若
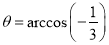 ,
,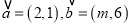 ,且
,且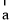 与
与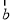 的夹角为锐角,求实数m的取值范围;
的夹角为锐角,求实数m的取值范围;(2)若
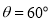 ,已知点
,已知点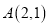 和直线
和直线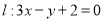 ①求l的一个法向量;②求点A到直线l的距离。
①求l的一个法向量;②求点A到直线l的距离。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
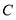 :
: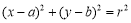 关于直线
关于直线 对称且过点
对称且过点 和
和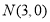 ,直线
,直线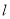 的方程为:
的方程为: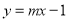 .
.(1)证明:直线
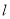 与圆
与圆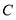 相交;
相交;(2)记直线
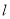 与圆
与圆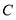 的两个交点为
的两个交点为 ,
,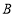 .
.①若弦长
 ,求实数
,求实数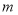 的值;
的值;②求
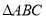 面积的最大值及
面积的最大值及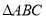 面积的最大时
面积的最大时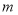 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的首项
 ,
,  ,
,  .
.(1)求证:数列
 为等比数列;
为等比数列;(2)记
 ,若Sn<100,求最大正整数n;
,若Sn<100,求最大正整数n;(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列,且am-1,as-1,an-1成等比数列?如果存在,请给以证明;如果不存在,请说明理由.
相关试题

