
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上的点.
上的点.

(1)若![]() 平面
平面![]() ,证明:
,证明:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)因为![]() ,利用线面平行的判定定理可证出
,利用线面平行的判定定理可证出![]() 平面
平面![]() ,利用点线面的位置关系,得出
,利用点线面的位置关系,得出![]() 和
和![]() ,由于
,由于![]() 底面
底面![]() ,利用线面垂直的性质,得出
,利用线面垂直的性质,得出
![]() ,且
,且![]() ,最后结合线面垂直的判定定理得出
,最后结合线面垂直的判定定理得出![]() 平面
平面![]() ,即可证出
,即可证出![]() 平面
平面![]() .
.
(2)由(1)可知![]() ,
,![]() ,
,![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() ,标出点坐标,运用空间向量坐标运算求出所需向量,分别求出平面
,标出点坐标,运用空间向量坐标运算求出所需向量,分别求出平面![]() 和平面
和平面![]() 的法向量,最后利用空间二面角公式,即可求出
的法向量,最后利用空间二面角公式,即可求出![]() 的余弦值.
的余弦值.
(1)证明:因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以可设平面
,所以可设平面![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
因为![]() 底面
底面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
综上,![]() 平面
平面![]() .
.
(2)解:由(1)可得![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在
所在
直线分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.
因为![]() ,所以
,所以![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.

设![]() 是平面
是平面![]() 的法向量,
的法向量,
由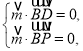 取
取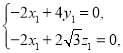
取![]() ,得
,得![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
由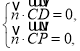 得
得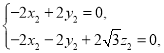
取![]() ,得
,得![]() ,
,
所以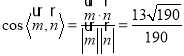 ,
,
即![]() 的余弦值为
的余弦值为![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体(semiregular solid) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为( )
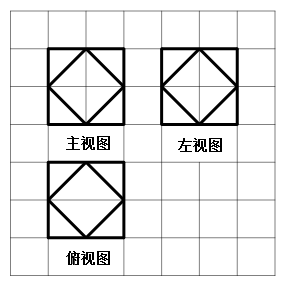
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).设
).设![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com