(本小题满分12分)定义在R上的奇函数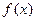 有最小正周期4,且
有最小正周期4,且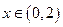 时,
时,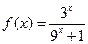 。
。
⑴求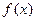 在
在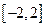 上的解析式;
上的解析式;
⑵判断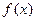 在
在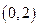 上的单调性,并给予证明;
上的单调性,并给予证明;
⑶当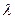 为何值时,关于方程
为何值时,关于方程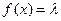 在
在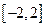 上有实数解?
上有实数解?
参考答案:
解:⑴当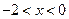 时,
时,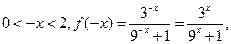
又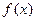 为奇函数,
为奇函数,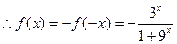 ,
,
当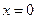 时,由
时,由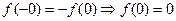
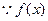 有最小正周期4,
有最小正周期4,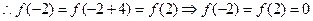 综上,
综上,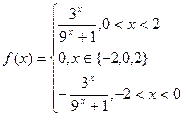
⑵设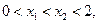 则
则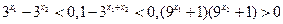
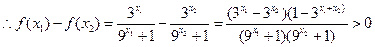
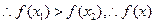 在
在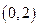 上为减函数。
上为减函数。
⑶即求函数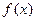 在
在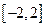 上的值域。
上的值域。
当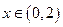 时由⑵知,
时由⑵知,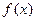 在
在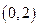 上为减函数,
上为减函数,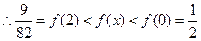 ,
,
当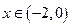 时,
时,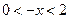 ,
,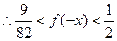 ,
,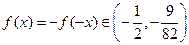
当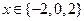 时,
时,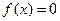
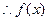 的值域为
的值域为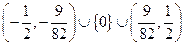
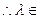
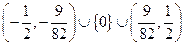 时方程方程
时方程方程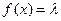 在
在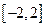
 上有实数解。
上有实数解。
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(14分)某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t-
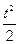 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润? -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)
(1)判断函数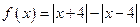 的奇偶性;
的奇偶性;
( 2)若
2)若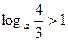 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>已知函数
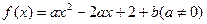 ,在区间
,在区间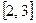 上有最大值5,最小
上有最大值5,最小
值2。
(1)求a,b的值。
(2)若 上单调,求
上单调,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)某企业生产甲、乙两种产品, 根据市场调查与预测, 甲产品
的利润与投资成正比, 其关系如图1, 乙产品的利润与投资的算术平方根成正比, 其关系如
图2 (注: 利润与投资 的单位: 万元).
的单位: 万元).
(Ⅰ) 分别将甲、乙两种产品的利润表示为投资的函数关系式;
(Ⅱ) 该企业筹集了100万元资金投入生产甲、乙两种产品, 问: 怎样分配这100万元资金, 才能使企业获得最大利润, 其最大利润为多少万元?
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知奇函数
 的定义域为
的定义域为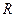 ,且
,且 在
在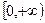 上是增函数, 是否存在实数
上是增函数, 是否存在实数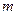 使得
使得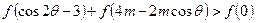 , 对一切
, 对一切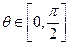
都成立?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)
某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次减少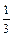 ,问过滤几次
,问过滤几次 才能使产品达到市场要求?
才能使产品达到市场要求?
相关试题

