【题目】定义:平面内两个分别以原点和两坐标轴为对称中心和对称轴的椭圆E1,E2,它们的长短半轴长分别为a1,b1和a2,b2,若满足a2=a1k,b2=b1k(k∈Z,k≥2),则称E2为E1的k级相似椭圆,己知椭圆E1: ![]() =1,E2为E1的2级相似椭圆,且焦点共轴,E1与E2的离心率之比为2:
=1,E2为E1的2级相似椭圆,且焦点共轴,E1与E2的离心率之比为2:![]() .
.
(Ⅰ)求E2的方程;
(Ⅱ)已知P为E2上任意一点,过点P作E1的两条切线,切点分别为A(x1,y1)、B(x2,y2).
①证明:E1在A(x1,y1)处的切线方程为![]() =1;
=1;
②是否存在一定点到直线AB的距离为定值,若存在,求出该定点和定值;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)①见解析;②存在一定点
(Ⅱ)①见解析;②存在一定点![]() 到直线
到直线![]() 的距离为定值1.
的距离为定值1.
【解析】
(Ⅰ)根据相似椭圆的概念,可得![]() ,
,![]() ,
,![]() ,然后根据
,然后根据![]() ,并结合离心率
,并结合离心率![]() ,简单计算,可得结果.
,简单计算,可得结果.
(Ⅱ)①联立方程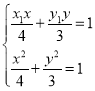 ,可得关于
,可得关于![]() 的一元二次方程,然后使用
的一元二次方程,然后使用![]() ,并根据
,并根据![]() ,可得结果.
,可得结果.
②根据①的结论,可得在点![]() 的切线方程
的切线方程![]() ,根据
,根据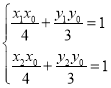 ,可得直线
,可得直线![]() 的方程,假设定点,使用点到线的距离公式,根据式子为定值,可得结果.
的方程,假设定点,使用点到线的距离公式,根据式子为定值,可得结果.
(Ⅰ)由题意知![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
而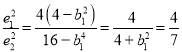 ,解得
,解得![]() ,
,![]() ,
,
故椭圆![]() ,椭圆
,椭圆![]() .
.
(Ⅱ)①联立椭圆与直线方程,
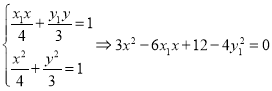 ,
,
点![]() 在椭圆
在椭圆![]() 上,有
上,有![]() ,
,
所以![]() ,
,
即直线与椭圆相切.
所以过点![]() 的切线方程为
的切线方程为![]() .
.
②由①知,过点![]() 的切线方程为
的切线方程为![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() ,
,
两条切线都经过点![]() ,则满足方程组
,则满足方程组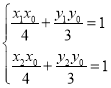 .
.
那么点![]() 和点
和点![]() 都在直线
都在直线![]() 上,
上,
则直线![]() 的方程为
的方程为![]() ,即
,即![]()
假设存在一定点![]() 到直线
到直线![]() 的距离为定值,
的距离为定值,
即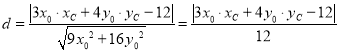 为定值,
为定值,
则![]() ,
,![]() ,
,
故存在一定点![]() 到直线
到直线![]() 的距离为定值1.
的距离为定值1.

