

【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕边AB翻转至
绕边AB翻转至![]() ,使面
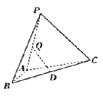
,使面![]() 面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
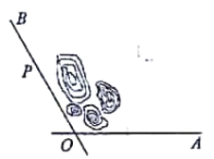
【题目】如图,一岛礁旁有两条航道![]() 与
与![]() ,
,![]() .一日,我方船只甲在
.一日,我方船只甲在![]() 航道上巡逻,在与
航道上巡逻,在与![]() 相距50公里的点
相距50公里的点![]() 处,发现不明身份的船乙刚驶过点
处,发现不明身份的船乙刚驶过点![]() ,并沿
,并沿![]() 方向以40公里/小时的速度运动,船甲立即沿
方向以40公里/小时的速度运动,船甲立即沿![]() 方向以
方向以![]() 公里/小时(
公里/小时(![]() )的速度追击,且甲到达点
)的速度追击,且甲到达点![]() 即停止前行(乙可继续前进).设甲出发时,经过
即停止前行(乙可继续前进).设甲出发时,经过![]() 小时甲,乙之间的距离为
小时甲,乙之间的距离为![]() 公里,当
公里,当![]() 最小时,可以达到最佳的驱离距离.
最小时,可以达到最佳的驱离距离.
(1)试求![]() 的解析式,并写出定义域;
的解析式,并写出定义域;
(2)求最多经过多长时间,我船可以达到最佳的驱离距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“完美区间”,另外,定义区间
的“完美区间”,另外,定义区间![]() 的“复区间长度”为
的“复区间长度”为![]() ,已知函数
,已知函数![]() ,则( )
,则( )
A.![]() 是
是![]() 的一个“完美区间”
的一个“完美区间”
B. 是
是![]() 的一个“完美区间”
的一个“完美区间”
C.![]() 的所有“完美区间”的“复区间长度”的和为
的所有“完美区间”的“复区间长度”的和为![]()
D.![]() 的所有“完美区间”的“复区间长度”的和为
的所有“完美区间”的“复区间长度”的和为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为1.
的面积的最大值为1.
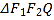
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() 且使
且使![]() 轴,如图,问四边形
轴,如图,问四边形![]() 的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)假设甲、乙、丙三名学生均获奖,且各自获一等奖和二等奖的可能性相同,求三人获得奖学金之和不超过1000元的概率.
附:回归方程![]() ,其中
,其中 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】马林●梅森是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为了纪念梅森在数论方面的这一贡献,将形如2P﹣1(其中p是素数)的素数,称为梅森素数.若执行如图所示的程序框图,则输出的梅森素数的个数是( )
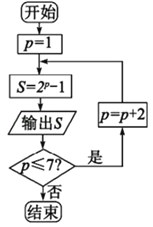
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,a∈R.
,a∈R.
(1)若函数f(x)在x=1处的切线为y=2x+b,求a,b的值;
(2)记g(x)=f(x)+ax,若函数g(x)在区间(0,![]() )上有最小值,求实数a的取值范围;
)上有最小值,求实数a的取值范围;
(3)当a=0时,关于x的方程f(x)=bx2有两个不相等的实数根,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() :
:![]() 经过伸缩变换
经过伸缩变换![]() ,后得到曲线
,后得到曲线![]() 以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为
以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为![]()
![]() 求曲线
求曲线![]() 的直角坐标方程及直线l的直角坐标方程;
的直角坐标方程及直线l的直角坐标方程;
![]() 在
在![]() 上求一点M,使点M到直线l的距离最小,并求出最小距离.
上求一点M,使点M到直线l的距离最小,并求出最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com